

Objective: Apply
the theorems and corollaries about isosceles triangles.
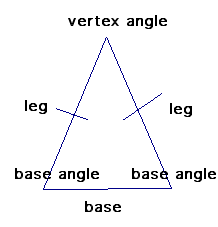
Defn: An isosceles triangle is a triangle with at least two congruent sides. These sides are called legs and the third side is called the base. The angles at the base are called base angles and the angle opposite the base is called the vertex angle of the isosceles triangle.
Isosceles Triangle Theorem:
If two sides of a triangle are congruent, then the angles opposite those sides are congruent.
Given: Segment AB congruent to Segment AC
Prove: Angle B congruent to Angle C
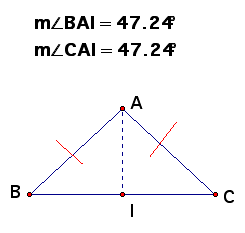
Plan for proof: Show
that Angle B and Angle C are corresponding parts of congruent
triangles. One way to do this is by drawing an auxiliary line
that will give you such triangles. For example, draw the bisector
of Angle A.
Corollaries of the Isosceles Triangle Theorem
Corollary 1: An equilateral triangle is also equiangular.
Corollary 2: An equilateral triangle has three 60 degree angles.
Corollary 3: The
bisector of the vertex angle of an isosceles triangle is perpendicular
to the base at its midpoint.
Converse of the Isosceles Triangle Theorem
If two angles of a triangle are congruent, then the sides opposite those angles are congruent.
Given: Angle B congruent to Angle C
Prove: Segment
AB congruent to Segment AC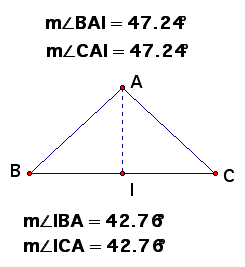
Plan for proof: Show
that Segment AB and AC are corresponding parts of congruent triangles.
Draw the bisector to Angle A as your auxiliary line, show that
angle AIB congruent to angle AIC and use ASA.
Corollary
An equiangular triangle is also equilateral.
Exercises
Write all proofs in two column format
1. Prove the Isosceles Triangle Theorem.
2. Prove the Converse of the Isosceles Triangle Theorem.
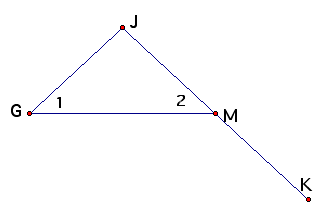
3. Given: M is the midpoint of segment JK; Angle 1 congruent Angle 2
Prove: Segment JG congruent MK
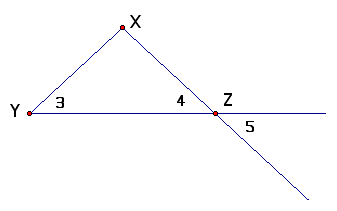
4. Given: Segment XY congruent XZ
Prove: Angle 3 congruent Angle 5
5. Given: Segment XY congruent XZ; Segment OY congruent OZ
Prove: Angle 1 equals Angle 4
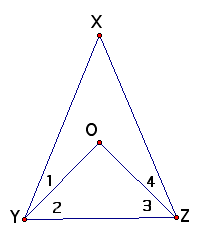
6. Given: Segment XY congruent XZ; Ray YO bisects Angle XYZ; Ray ZO bisects Angle XZY
Prove: Segment YO congruent ZO