

Have you ever been in a situation
where you are trying to show the validity of something with a
limited knowledge? I hope you have not. Why? Because, you just
have to use your ingenuity. Let's see...
Almost
everyone has studied (or seen) conic sections, particularly "parabola" in
his/her life. Most of us can remember at least the equation of
a parabola as y = ax ^2 + bx + c, and, you most probably
can draw the graph of most simple ones. Think about a situation
where you do not know "coordinate geometry", "calculus
in the modern sense (differentiation, integration etc...)".
You just know the definition of a parabola. You want to discover
certain properties of the parabola, and solve a problem. History
has lots of examples of this kind of situation. Wherever you go
in the written history of human beings, you will find that civilizations
built up with mathematics. With this respect, I think we must
teach mathematics with a little bit history (of mathematics).
We need to learn and teach to our kids how the concepts in mathematics
are developed. And I think this will allow to pupils to get a
broad vision of mathematics as well as a well built mathematical
thinking.
That is why I intended to write
an essay on "Quadrature of Parabola" which is
a famous work of Archimedes
(B.C. 287-212) well known with his words "Eureka, Eureka-I
have found it". The "Quadrature of Parabola"
is one of his works besides crying "Eureka." This work
of Archimedes has an important place in the history of mathematics
since there appear the ideas of limit and integration.
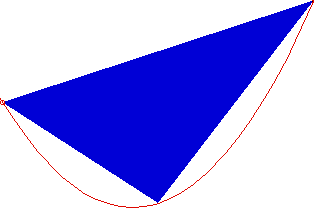
Quadrature of Parabola: The quadrature of the parabola investigates the ratio between the area of the parabolic section bounded by a parabola and a chord and the area of the triangle which has the vertex of the parabolic section and two points of intersection of the segment and the parabola as its vertices (See Figure-1).
|
|
The significance of the Archimedes' solution to this problem is hidden in the fact that none of differention, integration, or coordinate geometry were known in his time. But, if you look at Greek mathematics carefully, they were using the idea of limit, or in other words "approximation".
Now let's start to Archimedes'
solution to Quadrature of Parabola
Let A be the midpoint of the segment SS'. And let E and E' be the foot of the parallels from S and S' on the tangent line at V to the line passing through the points A and V. Take B as the mid-point of the segment VE and construct the segment BA' so that BA' is parallel to the segment AV. Similarly take B' as the mid-point of the segment VE' and construct the segment B'A'' so that B'A'' is parallel to the segment AV.
Construct the points C and D where the segment BA' intersect the parabola and the segment VS respectively. Similarly, Construct the points C' and D' where the segment B'A'' intersect the parabola and the segment VS' respectively.
|
|
Claim-I: The area of the triangle VCS is equal to the one-fourth of the area of the triangle VAS.
Proof: Since BA' is parallel to the segment VA (and so to the segment ES) and B is the midpoint of VE (i.e. VB/VE = 1/2), by Proposition-II,
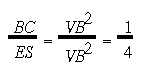 (1)
(1)Since BD = ES, BD = 4BC from (1).
|
|
|
If we consider Figure-3a and -3b which are extracted from Figure-2. The triangles VBD and VES are similar by A.A.A. (or A.S.A.) since BD//ES (and VE = 2 *VB). Therefore, BD/ES = VB/VE = 1/2. Since VESA is a paralleogram by construction, BA' = ES and BA'= 2BD .
On the other hand, since BC /2BD = BC/BA' = 1/4, BD = 2BC. In other words,
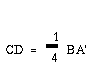 (2)
(2)
Now, if we look at the triangles VCA' and SCA', we may observe that have the same altitude (since VESA is a parallelogram and B and A' are the midpoints of the sides VE and SA respectively). On the other hand, since DA'= 2CD,
Similarly,
Adding up the areas,
Since A(![]() VAS)
= 2(
VAS)
= 2(![]() SA'V) and A(
SA'V) and A(![]() VCS)
= A(
VCS)
= A(![]() SDC) + A(
SDC) + A(![]() VCD),
then
VCD),
then
Then we are done.
Claim-II: The sum of the areas of the triangles VCS and VC'S' is one-fourth of the area of the triangle SVS'.
Proof: If the same argument applied to the left side of the Figure-2,
Therefore,
Now, since B and B' are the mid-points of VE and VE', respectively, Proposition-III asserts that C and C' are the respective vertives of the parabolic sections VCS and VC'S'.
Consider now the two parabolic
sections VCS and VC'S' with their circumscribed parallelograms
(See Figure-4). Applying Claim-II each of them shows that area
of the triangle VCS is four times the sum of the areas of the
two blue triangles at right. Similarly, the area of the triangle
VC'S' is four timesthe sum of the areas of the two blue riangles
at left. Since we have seen that A(![]() SVS')
= 4 (A(
SVS')
= 4 (A(![]() VCS) + A(
VCS) + A(![]() VC'S')),
the four blue triangles together have area
VC'S')),
the four blue triangles together have area
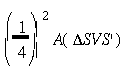
|
|
Let A = Area ![]() SVS'.
Recalling that the light blue area in Figure-2 is
SVS'.
Recalling that the light blue area in Figure-2 is
and that of Figure-4 is
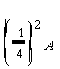
The process (forming triangles) can be repeated again and again. Thus the sum the blue triangles approximate the area of the parabolic section (See the Figure below)
 |
 |
 |
|
|
|
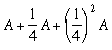 |
In other words,
![]()
Claim-III:
![]()
Proof: Click Here for
a demonstration !...
Thus,
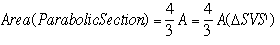
Click Here for a little example of "Quadrature of the Parabola" carried by Mapple...
Back
to EMAT 6690 Class Page
A. Kursat ERBAS © 2000
mail: aerbas@coe.uga.edu
This page created February 21, 2000
This page last modified March 6, 2000