Almost everybody knows about "Cartesian Coordinates". Yes, basically the cartesian coordinate of a point P is the pair (x , y) where x and y are the feet of the projection lines on the x and y axes respectively. This is a very basic way of locating a point in the plane. But, as we should know there is more than one way of showing a truth in mathematics. Here comes "Polar Coordinates" :

In the plane we choose a fixed point O, and we call it the pole. Additionally we choose an axis x through the pole and call it the polar axis. On that x-axis, there is just 1 vector E such that abs(E)=1. The pole and the polar axis constitute the basis of the polar coordinate system.

On the line OP we choose an axis u. The number t is a value of the angle from the x-axis to the u-axis. The number r is such that P = r.U The numbers r and t define unambiguous the point P. We say that (r,t) is a pair of polar coordinates of P.

One point P has many pairs of polar coordinates. If (r,t) is a pair of polar coordinates, (r, t + 2.k.pi) is also a pair of polar coordinates and additionally (- r, t + (2.k+1).pi ) is a pair of polar coordinates too. Of course, k is an integer. The polar coordinates of the pole O are by definition (0,t) with t perfectly arbitrary.

Consider a connection between the polar coordinates of a point and suppose, that connection can be expressed in the form F(r,t)=0 or maybe in the explicit form r = f(t). Such equation is a polar equation of a curve.

In this write-up we will try to investigate several properties of a very special polar equation:

where a, b and k are real numbers.

Obviously the easiest starting way in our investigation is taking a=b=k=1 and then keeping a=k=1 and playing with b. Now in Figure 1, we have seen several graphs of .

Figure 1a Click On

Figure 1b Click On

Figure 1c

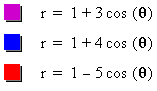As we may observe from Figure1a, when a=b=k=1, the graph of looks like a hearth and the graph intersect x-axis at x=0 and x=2 while it intersect y-axis at y=-1 and y=-2. In fact the graph in Figure 1a is so called "the cardioid", a name first used by de Castillon in a paper in the Philosophical Transactions of the Royal Society in 1741, is a
curve that is the locus of a point on the circumference of circle rolling round the circumference of a circle of equal radius. Of course the name means 'heart-shaped'.

In Figure 1b, we observe that when a=k=1, and b=2, the graph preserves the "cardioid" part and added a small loop intersecting x-axis at x=1. Ant the cardioid part of the graph intersect x-axis at x=0 and x=3. In fact, this graph is so called as "limacon".

On the other hand, when we look at the Figure 1c, we have seen that, fixing a=k=1 and letting b= 3, 4, and -5 produce some other limacons having similar properties. In fact, when b is negative the limacon reverse. One common property of all of the graphs in Figure1a is that all of them intersect y-axis at y=- and y=1.

So far, we have investigated the graphs in case, Ia/bI<2. So what exactly happens to the graph ofwhen Ia/bI<2 or Ia/bI=2.

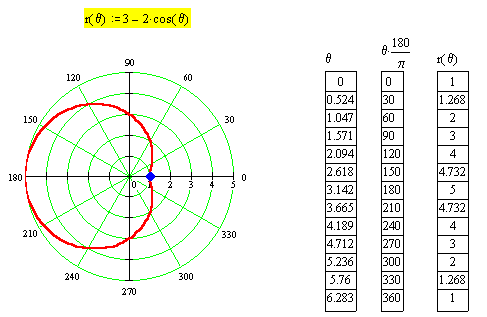
Here is an example: The graph of (See Figure 2)

Figure 2
Click On	Click On

As we may observe, the graph looks like a limason which is different than the ones above. First of all, since the sign of b is negative, the graph follows a loop from positive to negative. In particular since at equal to zero and 2pi (=6.28 in radians), the value of r in is 1 (see the data next to the graph in Figure 2), the graph starts from 1 and then while takes values from 0 to 2pi, r takes values from 1 to 1. So, it makes a loop like in the graph.

Actually, we can see what exactly happens to the graph according to the ratio between a/b can be demonstrated by a very nice movie clip. But first look at Figure 3a, 3b, 3c, 3d below.

Figure 3a	Figure 3b	Figure 3c	Figure 3d
Are you wondering what is going on? Click On

So far, we kept k=1 in . So, what happens if we give values other than '1'? First, we will try to substitute integer values for k (See Figure 4)

Figure 4

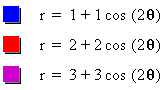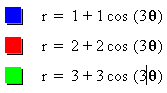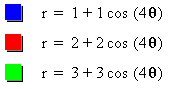As we see from Figure 4, when we keep a=b and letting k=n, where n is an integer, the graph of our polar equation is an n leaf rose. According to the values of a=b, the size of the n-leaf rose increase or decrease. But, all of the graphs remains concentric n-leaf roses.

But, what happens if a and b are different while k is fixed. So, see Figure 5a and 5b below.

Figure 5a, 5b

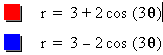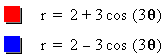As we may observe from the Figure 5a and 5b, when Ia/bI>1, we again get a n-leaf rose but its center is not origin. In fact, it becomes a wider n-leaf rose. When when a/b <0, then the rose is rotation of the rose in the case a/b >0. On the other hand, when Ia/bI increase, the shape of the rose approaches to a circle centered at origin with radious IaI.

Some interesting observations about the mathematical roses can be derived by taking a=0 and playing around r=bcos(). To see a movie clip for this:

Click On

---

May be another interesting point in this investigation what happens if we replace cosine function with sine function. Can you guess what happens? Can't?Maybe Figure 6a and 6b helps?

Figure 6a

Figure 6b

As we may observe, in the case a=b=k=1, if we replace cosine with sine, we get a cardioid rotated 90 degrees in counter clocwise. To see a movie clip:

Click On

Observing these facts,we may guess that the graphs of are the rotations of the ones in .

To see more examples, Click on the movie icons below:

---

This page created November 11, 1999

This page last modified November 13, 1999