

"Once upon a time, a mathematician deals with rabbits for the sake of their contribution to mathematics..."
Kursat
Fibonacci; the "greatest European mathematician of the middle ages", his full name was Leonardo of Pisa, or Leonardo Pisano in Italian since he was born in Pisa (Italy), the city with the famous Leaning Tower, about 1175 AD.
He called himself Fibonacci [pronounced fib-on-arch-ee or fee-bur-narch-ee] short for filius Bonacci which means son of Bonacci. Since Fibonacci in Latin is "filius Bonacci" and means "the son of Bonacci", two early writers on Fibonacci (Boncompagni and Milanesi) regard Bonacci as the family name so that Fib-Bonacci is like the English names of Robin-son or John-son. Fibonacci himself wrote both "Bonacci" and "Bonaccii" as well as "Bonacij"! Others think Bonacci may be a kind of nick-name meaning "lucky son" (literally, "son of good fortune"). He is perhaps more correctly called Leonardo of Pisa or, using a latinisation of his name, Leonardo Pisano. Occasionally he also wrote Leonardo Bigollo since, in Tuscany, bigollo means a traveller.
In Fibonacci's book he introduces a problem for his readers to use to practice their arithmetic:-
a pair of rabbits are
put in a field and, if rabbits take a month to become mature and
then produce a new
pair every month after that, how many pairs will there be in twelve
months time?
He assumes the rabbits do not escape and
none die. The answer involves the series of numbers:
1, 1, 2, 3, 5, 8, 13, 21, ...
Fibonacci Series is formed by starting with 0 and 1 and then adding the latest two numbers to get the next one:
| n: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
12 | 13 | 14 | |
| Fibonacci(n): | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | more.... |
We can write a general formula to generate a Fibonnaci sequence using
If we take the ratio of two successive numbers in Fibonacci's series, (1, 1, 2, 3, 5, 8, 13, ..) and we divide each by the number before it, we will find the following series of numbers:
1/1 = 1, 2/1 = 2, 3/2 = 1·5, 5/3 = 1·666..., 8/5 = 1·6, 13/8 = 1·625, 21/13 = 1·61538...
More formally, if we take the Fibonacci sequence as f(n) = f(n-1) + f(n-2), we get:
![]()
If we want to look at the convergence of the ratio f(n)/f(n-1),
When ![]() we
may write the above equation in limits:
we
may write the above equation in limits:
![]()
If we solve the equation we may get x is equal to
![]()
The constant![]() is
called "Golden Ratio", or "Divine Ratio" or
"Extreme Ratio". And 0,61803399... is called the reciprocal
of the Golden Ratio.
is
called "Golden Ratio", or "Divine Ratio" or
"Extreme Ratio". And 0,61803399... is called the reciprocal
of the Golden Ratio.
We will call the Golden Ratio (or Golden
number) after a greek letter,Phi (![]() ) here,
although some writers and mathematicians use another Greek letter,
tau (
) here,
although some writers and mathematicians use another Greek letter,
tau (![]() ). Also, we shall use phi (note
the lower case p) for a closely related value.
). Also, we shall use phi (note
the lower case p) for a closely related value.
It
is easier to see what is happening to ratio f(n)/f(n-1) if we
plot the ratios on a graph using MS Excell Spreadsheet (See Figure
1a, 1b, 1c):
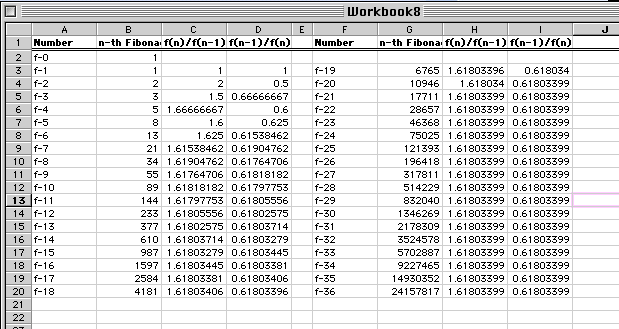 Figure 1a Figure 1a |
|
|
As we see from the graph, the ratio f(n)/f(n-1)
converges to the golden ratio ![]()
One immediate question arise: "What happens to the ratio f(n-1)/f(n)?"
In other words: What happens if we take the ratios the other way round i.e. we divide each number by the one following it: 1/1, 1/2, 2/3, 3/5, 5/8, 8/13, ..?
Again using spreadsheet environment, we may get Figure 2.
|
|
As we may observe from the Figure 2, the
ratio f(n-1)/f(n) is 0,618033989... which is the reciprocal of
the golden ratio.
The Fibonacci series starts with f(0)=1 and f(1)=1. If we want
to explore sequences where f(0) and f(1) are some arbitrary integers
other than 1.
For example, If f(0)=1 and f(1) = 3, then our sequence is a Lucas Sequence (See Figure 2a).
|
|
Again if we draw the graph of the ratios L(n)/L(n-1) and L(n-1)/L(n), we get the graph in Figure 2b:
|
|
As we have observed, the corresponding ratios of the successive terms in both Fibonacci Series and Lucas Series have the same rations. In other words:
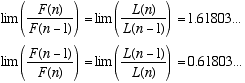
EXERCISES for Challenge:
1. Try some other starting values of your
own for a serie S(n) = S(n-1) + S(n-1).
2. Investigate what happens to the ratio of successive terms in
the series of the earlier questions. We know that for the Fibonacci
series, the ratio gets closer and closer to Phi = (sqr(5)+1)/2
(or Phi = (sqr(5)-1)/2. Does it look as (oh dear, I feel a pun
coming on: Lucas ![]() ) if all the series,
no matter what starting values we choose, eventually have successive
terms whose ratio is Phi?
) if all the series,
no matter what starting values we choose, eventually have successive
terms whose ratio is Phi?
This page created November 7, 1999
This page last modified November 7, 1999