

Long before the first pencil and paper, some curious person drew a triangle in the sand and a line from each vertex to the midpoint of the opposite side. To his or her amazement, the three connecting lines met in a single point. If you try it right now, the same thing will happen, no matter what shape of triangle you start with. The special point is called the centroid of the triangle. Think of it as the first triangle center, historically and conceptually.
The CENTROID (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side. Figure 1 shows the Centroid of different triangles. As it is obvious G is always inside the triangle whether it is acute, obtuse or right.
|
|
Click
here for
a GSP sketch showing CENTROID with animation
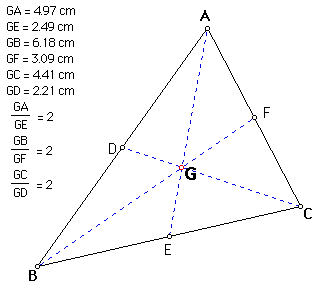 |
As it is seen from figure 2 that G divides a median into two pieces such that the distance from G to a vertex is twice the distance from G to the midpoint of opposite side of this vertex. In other words, using the same notation in Figure 2,
GA = 2GE, GB = 2GF and GC = 2GD.
This rule does not change in any triangle. Don't you believe me? Then Click Here for a GSP demonstration.
If you are not satisfied with
this demonstration let's present a formal proof of this theorem
concerning this fact.
Theorem: Prove that the three medians of a triangle are concurrent and that the point of concurrence, the centroid, is two-thirds the distance from each vertex to the opposite side.
Proof:
|
|
Let ABC be a triangle and D and F be the midpoints of AB and AC respectively.
In triangles ADF and ABC, since <DAF = <BAC and AB = 2AD and AC = 2AF, they are symmetric by Side-Angle-Side Symmetry Theorem. It immediately follows that <ADF = <ABC and <AFD = <ACB, i.e. DF//BC. (1)
In triangles GFD and GBC, since DF//BC (See 1), <GFD = <GBC, <GDF = <GCB (from the property of alternate interior angles) and <DGF = <CGB (from sum of the angles of a triangle, which is 180). Therefore, it follows from Angle-Angle-Angle Symmetry Theorem that the triangles GFD and GBC are symmetric.
So, we have ![]() or
or
![]() .
.
Similarly, median CD intersects BF at G so
that ![]() .
.
If we repeat the same calculations for the pairs of medians AE & CD, and AE & BF, we see they intersects at a point such that it cuts a median into two pieces so that the piece closest to the side is half of the piece closest to the vertex. That point could be one, and it is G.
Click Here for an animation of the construction of the above
proof.
Centroid (G) is also known as the "Center of Gravity" of a triangle.
The Center of Gravity (C.G.) is merely the balancing point of an object. For instance, the C.G. of a 10 inch stick is 5 inches. If the stick is made of the same material and has the same weight inch-for-inch, it will balance when supported or pivoted at its 5 inch mark. Stated another way, gravity is pulling the stick down with equal force on each side of the 5 inch mark, but because the stick is supported at this mark and the weight of the stick is the same on either side of the mark, the stick will balance and assume a true horizontal position.
Click Here for a proof in which there is shown that centroid
(G) is really the center of gravity of a triangle.
Another interesting property of centroid is that the medians divides a triangle ABC into six small triangles having equal areas.
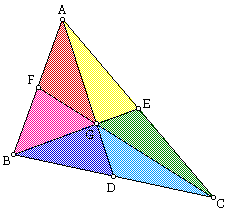 |
Click here for an interactive exploration of this fact: the medians divides a triangle ABC into six small triangles having equal areas.
Proof:
Exercise (Hint: Use the formula A=1/2.a.b.sin(x))
At this point it would be nice to mention about some possible use of GSP in geometry courses.
One of the difficulties of students (and most people) in geometry is inabilty to drow nice figures of geometric objects which leads to inability to see the relations between the figures and objectss. This becomes more clear when one should drow more than one geometric object together. However, with using GSP, this problem can be solved easily. It is easy to use (very basic menus, and etc), so students can use it effectively to drow nice figures.
Another difficulty of students is that most of them could not be able to imagine different orientation of the figures. For example, to judge whether the truthness of a fact or relation valid for acute triangles is valid or not for obtuse triangles, most of the students can not judge it in their minds and should drow another figure and look. However, it is easy to manipulate and animate object in GSP. So, students can easily investigate a problem from different perspectives. On the other hand, it is easy to make simple calculations (calculating distances, angles, basic functions and etc.) in GSP. So students can look the truthness of some relations that they think it might exist or they can discover some relations by just trial and error.
We can use GSP in geometry classes in everywhere even in proofs. For example, if we take above proof, introduce the topic of medians and give some important definitions. Then ask students what they can discover about the medians of a triangles after drowing a triangle and its medians. And ask if these properties cn hold everytime in every situation. At last, want from them to list what they have discovered and connect these with some other properties of midpoints and properties of triangles. You may direct students to make a poof of what they found just by giving clues.
In sum GSP is a very nice tool for geometry
for classroom and personal uses.
This page created September 18, 1999
This page last modified September 25, 1999