In this page, we try to present a solution for a very famous problem. The problem was proposed by P.Fermat (1665-1601).

Now, let present the problem itself and a solution for it:

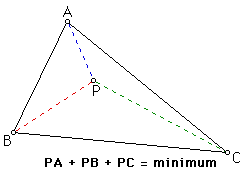
Problem: Consider any triangle ABC. Find a construction for a point P such that the sum of the distances from P to each of the three vertices is a minimum. In Figure 1, this problem is visualized.

Figure 1 Click here to play a GSP file for this skecth.

Solution:

In the triangle ABC (above), select a point P and connect it with vertices A, B, and C.

Rotate the triagle ABP 60 degrees around B into position A'BP'. By construction, BPP' is equilateral, BP = BP', and AP = A'P'. We thus have: PA + PB + PC = P'A' + P'P + PC.

As the image of A under the rotation, position of A' does not depend on P. Also, PA + PB + PC is greater than or equal to CA' because the broken line CPP'A' is no shorter than the straight line CA'.
Therefore, PA + PB + PC reaches its minimum iff P lies on CA'.
For this P, BPA' = 60 degrees. Had we rotated ABP around A, we would have found that APA' = 60 degrees.

On the sides of the triangle ABC construct equilateral triangles ABA', ACC', and BCB'. We know that the point P minimizes the sum PA + PB + PC lies on CA'. By the same token, it lies on BC' AB'. Therefore, it lies on their intersection. If we construct these three lines AB', BC', and CA' are concurrent. Not only that but they cross at angles equal 120 degrees (See Figure 3).

Figure 3

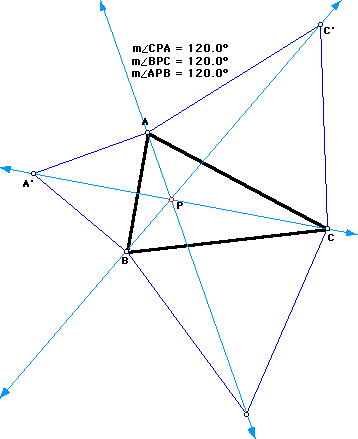
The Fermat point is the locus of the intersection of the line from the vertices of the triangle to the vertices of the externally constructed equilateral triangle on the opposite side. In fact, this intersection point is called the First Fermat Point. With the above construction, Although the First Fermat Point remains inside the triangle if one of the angles of the triangles is less than 120 degrees, it is outside the triangle if one of the angles of the triangle is bigger than 120 degrees. Moreover, if one of the angles is 120 degrees, then the First Fermat Point is the vertice where the angle is 120 degrees.

As we may observe from Figure 4, when we move the vertex A, the locus of the First Fermat Point is a circle which is, in fact, the circumcircle of the triangle BB'C. Therefore, the radius of this circle is the radius of the circumcircle of the triangle BB'C. Since BB'C is equilateral, the radius is equal to BC.

Similarly, we may expect that when we move the vertex B, the locus is the circumcirle of the triangle ACC' and it is the circumcirle of the triangle AA'B when we move the vertex C. And, the same radius discussion can be applied to these triangles.

From this discussion, we may conclude also that, the First Fermat Point is the intersection of the circumcircles of the triangles BB'C, ACC', and AA'B.

Click here for an interactive investigation with GSP.

Proof: The proof of the above statement comes from two facts we have found above:

The angles APC, APB, and BPC are always fix and equal to 120 degrees when the largest angle of it less than 120 (APC, APB, and BPC are 120, 60, 60 in some permutation if the largest angle is bigger than 120 degrees. For example, if B>120, APC=120 degrees and the others are 60 degrees each.)

The triangles AA'B, BB'C and CC'A are equilateral.

Since the angles APC, APB, and BPC are fixed and while B, C, A are moving they always see the fixed sides AC, AB and BC of the triangle ABC, they are on the circumcircles of the triangles AA'B, BB'C and CC'A.

The Fermat point is also known as the 1st isogonic center, the roots iso and gon meaning equal-angle. This is because the angles BPC, CPA, APB are all equal. (The 2nd isogonic center is obtained using the other three equilateral triangles on the sides of triangle ABC.)

The Second Fermat Point is the concurrency of lines drawn from the vertices of the triangle to the vertices of equilateral triangles constructed INWARDLY on the opposite sides (See Figure 5).

This page created September 26, 1999

This page last modified December 18, 1999