

Definition: Let triangle
ABC be any triangle. Then if P is any point in the plane, then
the triangle formed by constructing perpendiculars to the sides
of ABC (extended if necessary) locate three points R, S, and T
that are the intersections. Triangle RST is the Pedal Triangle
for Pedal Point P.
Figure 1 shows the construction of the pedal triangle (RST, blue triangle) given the point P outside the triangle ABC.
|
|
Click Here for a GSP script for constructing the pedal triangle to triangle ABC with point P (inside or outide of ABC)
As one can expect, according to the point P, the pedal triangle can be inside or outside of ABC. Even sometimes it can be a degenerate triangle?... Let's try to investigate some properties of the pedal triangle.
As we know, there are some special points (centers), and related circles (circumcircle, nine-point circle etc) for a triangle such as centroid, incenter, orthocenter etc. When we mention about the pedal triangle for a given pedal point P, we may wonder what if the pedal triangle coincides with one of these special points?
Now let's try to investigate some of the properties of pedal triangles according to the pedal point.
What if pedal point P is
the centroid of
triangle ABC?
As we remember, centroid of a triangle ABC is the intersection of its medians. If we draw perpendiculars to the sides of the triangle ABC, and connect the feet and get the pedal triangle.
The question is: Is there any relation you see?
Answer is simple: No.
If you do not believe me, Click Here to try and see yourself.
What
if . . . P is the incenter
. . . ?
As we know, incenter I of ABC is simply the intersection of the angle bisectors. The Figure 2 illustrates what happens if P is the incenter (I) of ABC.
|
|
Observation-1: When P is the incenter of a triangle ABC, the incircle of ABC is the circumcircle of the pedal triangle with pedal point P.
In other words, the incenter I of ABC is the circumcenter C of the triangle RST.
Proof: Let PR, PS and PT be the perpendiculars drawn from P to the sides AB, BC and CA of a triangle ABC.
Then the triangle TPC and SPC are congruent from A-A Similarity Theorem. Thus, d(PT) = d(PS).
Similarly, the triangles PTA and PRA are congruent from A-A Similarity Theorem. Thus d(PT) = d(PR).
Therefore, d(PT) = d(PS) = d(PR). Thus a circle (Look at the red circle in Figure 2) passing through the points R, S and T is tangent to the sides of the triangle ABC and circumscribe the triangleRST.
Thus the incircle of ABC is the circumcircle of the pedal triangle RST with pedal point P.
Observation-2: When P is on the incircle of the triangle ABC, then the loci of the vertices of the pedal triangle are segments having lenght equal to the diameter of the incircle.
In fact the segments are the "projections" of the circle to the three sides of the triangle.
It is a nice observation. At this point one can think whether
it is true for all cases?
Well. I have tried this in different cases and I have observed the same thing.
If you wonder about it: Click Here for a GSP demonstration to try and see youself.
|
|
Proof: To construct the segment on the side AB of the triangle ABC, first construct the line L through the center O of the incircle such that L is parallel to AB. Let Q and R be the points of intersection of L and the incircle. Let M be the line through P perpendicular to AB, and let S1 be the intersection of M with AB. Let N be the line through Q perpendicular to AB, and let S2 be the intersection of N with AB. Then S1S2 is the segment on the side AB.
The construction of other segments are similar.
Note: Thanks to Dr. Macrory (clint@math.uga.edu) for his help on this construction
What if . . . P is the Orthocenter . . . ?
Figure 4 illustrates the position of the pedal triangle RST when P is on the orthocenter H of ABC.
|
|
From the definition of pedal triangle and orthic triangle that the pedal triangle RST is the orthic triangle of ABC when P is on the orthocenter H of ABC.
If H is outside of the triangle ABC, then the
two vertices of RST is outside the triangle.
What if . . . P is the Circumcenter and on Circumcircle. . . ?
Figure 5 illustrates the the position of the pedal triangle RST when P is on the circumcenter C of ABC.
|
Figure 5. P is the circumcenter of ABC |
Observation: When P is the circumcenter(C) of a triangle ABC, the feet of the pedal triangle are the midpoints of the sides of the triangle. And so the pedal triangle is the medial triangle in this case.
Proof: The proof of this observation is quite easy. They follows from just the definitions of the pedal triangle, medial triangle, and circumcenter.
An interesting observation for a pedal triangle is when the pedal point P is on the Circumcircle of a triangle ABC. If it is the case, the pedal triangle is a degenerate triangle. In other words, it is just a line segment, which is called Simson Line. (See Figure 6 )
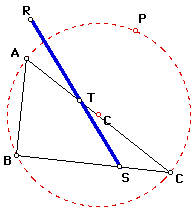 Figure 6. P is on the circumcircle of ABC |
Notice that since there are infinitely many points on the circumcircle of a triangle, there are infinitely many Simson Lines of the triangle.
Therefore, one can wonder "if there is any relationship between the simson lines of several points on the circumcircle?"
Of course to discover some relationships GSP will help us.
|
|
Observation: The Envelope of the Simson lines of a triangle is a Deltoid (See the animated gif in Figure 7b).
|
|
Each side of the triangle is tangent to the Deltoid at a point whose distance from the Midpoint of the side equals the chord of the Nine-Point Circle cut off by that side (Wells 1991, p. 231).
If we observe the behavior of two simson line, they may intersect. But an interesting observation is this:
Observation: The Simson lines of two opposite points (opposite ends of a diameter) on the Circumcircle of a triangle are Perpendicular and meet on the Nine-Point Circle.
This observation can give an idea to investigate the angle between simson lines of two points which are not opposite in a diameter of circumcircle. One guess may follow from the fact in above observation that the measure of the arc P1P2 is 180 (since P1P2 is a dimater) and the angle between simson points is 180/2 = 90 (see Figure 7). Therefore, we may guess that:
Observation: The Angle between the Simson lines of two points P and P' is half the Angle of the arc PP'. (See Figure 8)
|
|
Observation: The Simson line of any Vertex is the Altitude through that Vertex
(See Figure 9a)
Observation: The Simson line of a point opposite a Vertex is the corresponding side (See Figure 9b)
|
|
|
If we look at the relation between simson line and other triangle center (orthocenter, center of nine- point circle and etc) we can observa that:
Observation: The Simson line of P bisects the line HP, where H is the Orthocenter Moreover, the Midpoint of HP lies on the Nine-Point (See Figure 10).
|
|
This page created October 16, 1999
This page last modified October 23, 1999