1) Using GSP (Geometer's Sketchpad), construct regular polygons with n sides for each of the following values: n = 3, 4, 5, 6,8, 12. In each case your given data should be two points, which will be the endpoints of a side of the polygon. You should also give a written description of your construction, step by step. (You do not have to prove that your construction works, however.) To construct a regular pentagon, you may want to use the outline given in class, based on a construction of the golden ratio.

Extra credit (required for grad students): Prove that for a regular pentagon the ratio of a diagonal to a side is the golden ratio.
(Hint: Use trigonometry.)

Solution:

We know that a regular polygon with 3 sides must have internal angles. Therefore, all we have to do is construct a equilateral triangle.

First draw AB line segment. And then draw circle 1 & circle 2 above by taking A and B points as a circle center and line segment AB as a radius. The intersection of these two circles is going to give us third point for our equilateral triangle. If we draw a segment between these three points, we will get 3 sided regular polygon (equilateral triangle).

We know that a regular polygon with 4 sides must have internal angles. Therefore, all we have to do is construct a square.

First draw AB line segment. And then draw circle 1 & circle 2 above by taking A and B points as a circle center and line segment AB as a radius. Third, draw 2 line from A and B points which are perpendicular to AB line segment. The intersection points of these two lines with our circles are going to give us third & fourth points for our square. If we draw a segment between these four points, we will get 4 sided regular polygon (square).

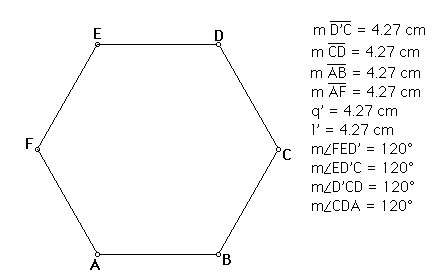
We know that a regular polygon with 6 sides must have internal angles. Therefore, all we have to do is find how to construct a angle.

First draw AB line segment. And then draw equilateral triangle ABC. Third, draw equilateral triangle AEC by drawing circle 2 & circle 3 above by taking A and C points as a circle center and line segment AC as a radius. The intersection of these two circles is going to give us third point for our equilateral triangle AEC. As you can see above, we will get the angle EAB which is exactly equal to . We will also get to sides (AB & AF). If we apply same procedure three times, we will be able to construct 6 sided regular polygon (hexagon).

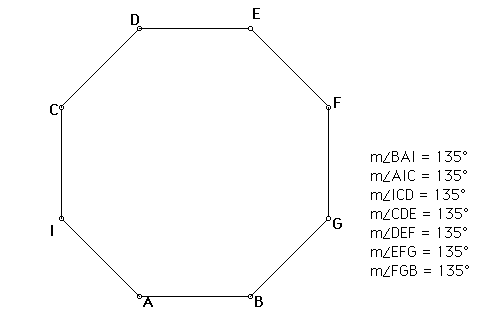
We know that a regular polygon with 8 sides must have internal angles. Therefore, all we have to do is find how to construct a angle.()

In order to construct a angle, we must construct angles. First draw AB line segment. And then draw a perpendicular line to line segment AB from point A. Now, as you can see figure above the angles FAB =FAG= . In order to find , I draw two circle by taking F & G points as center and line segment FA and GA as a radius. The intersection of these two cirle is going to divide angle FAG = into two equal angle. (See figure above) If we draw circle 2, the line segment IA will be equal to AB. The angle IAB is going to equal to .If we apply same procedure again and again, we will be able to construct 8 sided regular polygon (octagon).

We know that a regular polygon with 12 sides must have internal angles. Therefore, all we have to do is find how to construct a angle.()

In order to construct a angle, we must construct angles. First draw AB line segment. And then draw a perpendicular line to line segment AB from point A. Now, as you can see figure above the angles CAB = . In order to find , I construct equilateral CAE triangle (See figure above). If we draw the line segment EA will be equal to AB. The angle EAB is going to equal to .If we apply same procedure again and again, we will be able to construct 12 sided regular polygon .

If you would like to see script file for this construction please CLICK HERE

At first, take any two points (A, B). Then draw the line segment between point A and point B. I draw circle 1 & circle 2 by taking point A and point B as a center and line segment AB as a radius. Find point C which is the midpoint of line segment AB. Draw a line from B point whic is perpendicular to line segmant AB. Find intersection of Circle 2 and this perpendicular ray. Draw another circle by taking point C as a center and line segment CE as a radius. Find the intersection of circle 3 and AB parallel line ( point G). Draw a line segment between G and B points. Draw another circle by taking point G as a center and line segment GB as a radius (circle 5). Find the intersection of circle 5 and circle 2. Find the intersection of circle 5 and circle 4. As you can see from the figure above, we get the location of 5 points for our 5 sided regular polygon. If we draw line segment between these points, we will get our regular 5 sided polygon (pentagon).

Prove that for a regular pentagon the ratio of a diagonal to a side is the golden ratio?

Let's take a regular ABCDE pentagon.

We know that in a regular 5 sided polygon all interior angles are equal to . In triangle AED, we know that ED=EA and m(AED)=. The triangle AED is a isosceles triangle and . If we apply sine theorem here we will get:

as one can easily see this valu exactly equal to golden ratio

Using the Cosine Theorem will give us the same result:

In triangle AED, . As we proved that in a regular 5 sided polygon the ratio of a diagonal to a side is always golden ratio no matter wahat is the length of one side.