

Write-up 12
An Exploration in Exponential Growth - Compound Interest
T. Barron
One of the most common examples of exponential growth is compound interest. Suppose that you have $100 that you could put either in a checking account that earns no interest, a NOW account that earns 3 % compounded annually, a savings account that earns 5% compounded annually, or a certificate of deposit that earns 7% compounded annually. How would your results compare after 10 years? After 25 years?
Assuming you make no withdrawals, the money in the checking account will remain constant at $100. The money in the interest-bearing accounts will obviously increase, but by how much?
At an interest rate of 3% compounded annually means that at the end of each year, you earn 3% on the current value of your account. The interest is automatically deposited into your account. From then on, you earn 3% not only on your principal (the initial amount you invested), but also on the interest you have already earned. The growth rate is 3% or 0.03 in decimal form, and the growth factor is 1.03. So, each year, the current value of the account will be multiplied by 1.03. The functions representing Pr, the current value of your account earning interest r, as a function of n, the number of years, would be:
P 0.03 = 100 · (1.03)n
P 0.05 = 100 · (1.05)n
P 0.07 = 100 · (1.07)n.
In general, if
Po = original investment
r = interest rate (in decimal form)
n = (time periods at which the interest rate is compounded per year),
the resulting value Pr, of the investment after n time periods is given by the formula:
Pr = Po · (1 + r)n.
The interest rate, r, in decimal form is the growth rate and 1 + r is the growth factor.
Using an Microsoft Excel, we can complete a table such as the Table 1 below to compare the values of the account over 10 years. At 10 years, the $100 in the 3% account has risen to $134.39, while the $100 in the 7% account has almost doubled to $196.72. The constant value of the $100 in the checking account is not listed, but appears in Table 1 as the flat line.
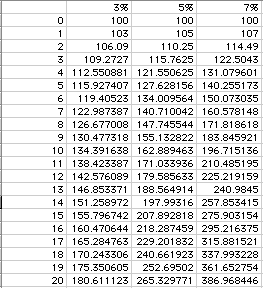
Table 1
The longer the time period over which you invest, the more dramatic the results. Over time, small differences in interest rates can produce enormous differences in returns. Table 2 and Figure 2 below show the value of $100 invested at 3%, 5%, and 7% over 40 years. If you invested $100 at age 25 for your retirement 40 years later at 3% compounded annually, you would end up with $326; at 5% you would have $704; and at 7% you would have almost $1500 or nearly 15 times as much as you started with. So, if you were able to invest $10,000 at 7% for 40 years, you'd have about $150,000. Explore with your students, the fact that no matter what the principle, the time required to double, triple, etc., the principle is the same when using the same rate and compound. For instance, the three amounts invested in as depicted in the table below are all invested at a rate of 12%. Notice that it takes the same amount of time for all amounts of money to double.
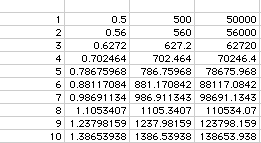
Table 2
A note about inflation:
At decent interest rates, if we could put aside a few thousand dollars each year, it seems that we could retire in comfort. Is the picture as rosy at it seems? Not quite. We haven't taken inflation into account. Compound interest calculations are the same whether you are dealing with inflation or investments. For example, a 5% annual inflation rate would mean that what cost $1 today would cost $1.05 on year from today.
If we think of three percentages in Table 1 ad representing inflation rates, then how much would something that costs $100 today cost in 10 years? It would cost $134.39, $162.89, or $196.72, if the annual inflation rate were 3%, 5%, or 7%, respectively. So, if you invest $100 at 5% for 10 years, it will be worth $162.89. However, inflation will drive up the costs. If, during those 10 years, inflation is also 5% a year, then what originally cost $100 will now cost $162.89. In terms of purchasing power, you will come out even, with no net gain or loss. So, if the inflation rate equals the interest rate, you are not any better off. If the inflation rate were higher that the interest rate, you would actually lose money on your investment. Because of the erosive nature of inflation, most economists usually use real or constant dollars, which are adjusted for inflation.
Something to think about with respect to inflation and the diminishing dollar.
Inflation erodes the purchasing power of the dollar. If you have $1.00 today and annual inflation is 5%, how much will the dollar be worth in a year? In an year, what cost $1.00 today, will cost $1.05. Since 1.00/1.05 = 0.952, the $1.00 = 0.952 · ($1.05). So in a year, $1.00 will be worth only 92.5 cents. The decay factor is 0.952. The exponential function:
D = 1 · (0.952)n
Gives D, the value (or purchasing power) of today's dollar, at year n in the future if there is a steady inflation rate of 5%. In economists' terms, it gives the real purchasing power in today's dollars.
Every 14 years, the purchasing power of your money is cut in half. We can thing of 14 years as the half-life of the dollar. So, in 14 years, your dollar is worth 50 cents. In 28 years, your dollar is worth only 25 cents. This is obviously a serious problem faced by those who retire on a fixed pension income.
A discussion for you and your students:
If you win $1,000,000 in say, a lottery, and receive $33,500 a year for 20 years, how much interest are you paying? Is this "fair"?