

When discussing characteristics of a quadratic function or a polynomial function of degree two, the equations are usually seen in one of two forms:
The first form, which is usually referred to as the standard equation of a parabola is
where a, b, and c are constants and a is not equal to zero.
The focus of this paper is to determine the characteristics of parabolas in the form:
For our purposes, we will call this second form the shift-form equation of a parabola.
Given a quadratic in this form, it is fairly easy to predict the general shape of the parabola. By examining a coefficient and the values for h and k, it is possible to determine the horizontal and vertical shift, the vertex, whether the parabola opens up or down, where the y-intercept is located, and whether the curve is generally flat or narrow.
The graph of the standard quadratic function, y = x2 is shown below in Figure 1.
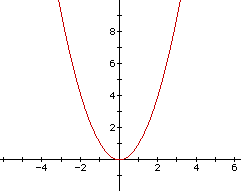
All other functions, including ones that shift horizontally and vertically, as well as those that open up or down and are either flat or narrow, will be based off of this standard parabola. Before discussing horizontal and vertical shift, it is necessary to determine other characteristics of the graph that depend on the "a" coefficient.
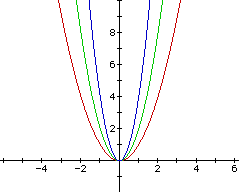
Note that in Figure 1, the parabola opens upward. In the graph below in Figure 2, notice what happens to the values of y when x is multiplied by 2 and then by 4. In comparing the graphs of y = x2 (red), y = 2x2 (green), and y = 4x2 (blue), we see that each parabola opens upward but the larger the value of "a", the steeper (narrower) the graph. Thus, when a ³ 1, the parabola opens upward, and as the value of "a" increases, the shape of the parabola narrows.
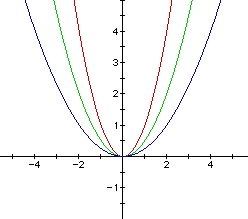
When 0 < a < 1, note that the smaller the numerical value of the fraction, the "flatter" the graph. Thus, depicting the graphs of y = x2 (red), y = (1/2)x2 (green), and y = (1/4)x2 (blue), as illustrated in Figure 3, as the fractions get smaller, the parabolas flatten-out and lie closer to the x-axis.
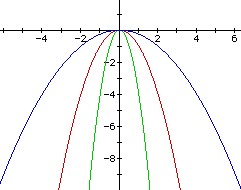
Conversely, when a £ -1, the graph opens downward and becomes narrower as the value of "a" decreases. When -1 < a < 0, as the | a | decreases, the graph flattens as depicted below. Figure 4 illustrates y = -x2 (red), y = -4x2 (green), y -(1/4)x2 (blue).
While the value of "a" determines whether the parabola opens upward or downward and whether it is narrow or flat, it has nothing to do, in general, with horizontal or vertical movement.
To learn how the parabola in standard form y = ax2 + bx + c relates to the parabola in the shift-form, y = a(x - h)2 + k, we can use the completing the square method in the first parabola to produce the equation:
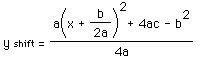
When graphing the parabola in standard form, to find the vertex we use the following method: The x-value of the vertex is calculated as x = -b/(2a). The y-value of the vertex is f(-b/(2a)). The x-value of the vertex also represents the horizontal shift, while the y-value represents the vertical shift. Thus, when looking at the shift-form of the graph, we see that -h = b/(2a) or h = -b/(2a), while k = (4ac-b2)/4a.
Here, a numerical example may be helpful. Thus, let's take, for example, y = x2 + 6x + 1. The horizontal shift and x-value of the vertex is -b/(2a) = -6/(2(1)) = -3. The vertical shift and the y-value of the vertex is f(-b/(2a)) = (-3)2 + 6(-3) + 1 = -8. Thus, the vertex is (-3, -8) which corresponds with the vertical and horizontal shift, respectively. Now, we can re-write this equation in the shift-form by completing the square or merely by following the y-shift equation above. Either way, the shift-form of the equation is y = (x + 3)2 - 8. Now, since the opposite of h is the horizontal shift, the horizontal shift is -3, NOT +3 as we may thing by glancing at the shift-form of the equation. However, the vertical movement, k, is (4ac - b2)/4a which equals -8.
Since algebraic manipulations of such equations are hard to grasp without a visual image, let's discuss the characteristics of several parabolas by graphing.
As stated previously, the graph of y=x2 is our standard graph. Also, y = x2 + h shifts the graph only up or down, depending upon whether the value of h is positive or negative, respectively. Thus, the graph of y = x2 + 2 (red) and y = x2 - 3 are illustrated below in Figure 5. Note the left and right shifts, respectively.
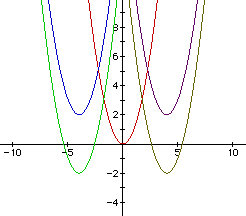
Now, let's look at the graphs of y = x2 (red), y1 = (x + 4) 2 - 2 (green), y2 = (x + 4) 2 + 2 (blue), y3 = (x - 4) 2 - 2 (brown), and y4 = (x - 4) 2 + 2 (purple). Notice that the graphs have vertices (0, 0), (-4, -2), (-4, 2), (4, -2), and (4, 2), respectively.
After talking with several colleagues about how they teach the horizontal and vertical shifts with respect to parabolas, I have found several methods ranging from algebraic manipulations of the formulas and graphical representations (above), to mnemonic devices to help their students memorize that the horizontal shift is the "opposite" of the number as it appears in the equation, and the vertical shift is the "same" as the number in the equation, or "normal". However, given the time and resources, I believe that students can benefit from seeing and graphing several parabolas similar to the ones in this paper, to determine the characteristics and how the shape of a parabola changes with changing values in the equation.