

First, let's discuss how to construct a pedal triangle. Let triangle ABC be any triangle. If P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) and the intersections of the perpendiculars and the sides is a pedal triangle. The pedal triangle for point P is depicted as the magenta triangle shown below.
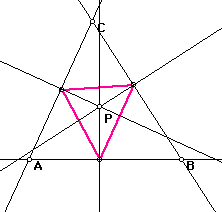
Now, the question is, what if P is the Circumcenter? As discussed previously, the Circumcenter of a triangle is the point in the plain equidistant from the three vertices of the triangle. Since, by definition, a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, the circumcenter is on the perpendicular bisector of each side of the triangle. Note that the circumcenter may be outside of the triangle as shown in Figure 3. In Figure 2 below, the circumcenter and the pedal point p are one in the same. By the characteristics of parallelograms, it is clear that triangle HIJ shares half of a parallelogram with triangles CHJ, HAI, and JIB. Thus, the area of triangle HIJ is equal to triangles CHJ, HAI, and JIB as indicated below. Thus, it follows that the area of HIJ is 1/4 of the area of ABC. Click here to manipulate the GSP construction below.
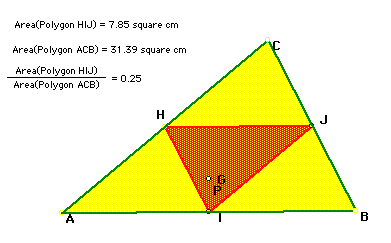
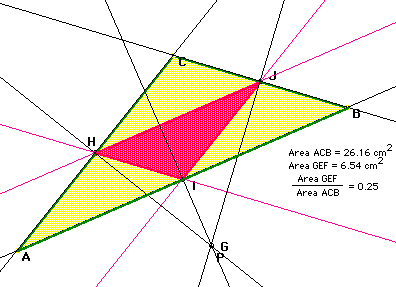
Figure 3 indicates that the 1/4 ratio holds even for pedal points superimposed on circumcenters outside of a triangle. This proof is similar to the proof mentioned above for circumcenters and pedal points inside the triangle. Click here to manipulate the GSP construction as illustrated below.
This characteristic of a pedal triangle, along with others mentioned in the overall scope of this write-up are excellent investigations for those students in any Geometry class.