Click to check the problems
from the previous lesson
We learned that in a right triangle the sum of the squares of the legs of the right triangle is equal to the square of the hypotenuse of the right triangle.
The ancient Egyptians used to form right angles by takinng a rope with
12 equally spaced knots. They would form a triangle with sides of length
of 3, 4 anf 5 knots. We know that 
, so does this prove
that the triangle they formed was a right triangle?
Activity: Open the GSP
sketch and record the values of 
and if the triangle
is acute,obtuse or right in your notebook.
What conjectures can you make?
If the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
Write the Converse Theorem and complete the proof in your Journal.
Given: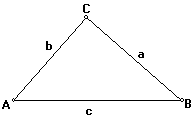 
ABC with 
Prove: ABC is a right triangle.
Outline of proof:
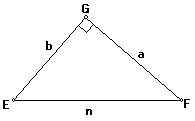
1. Draw a right triangle EFG with legs a and b
2.
(why?)
3. (Given)
4.c = n (why?)
5.ABC 
EFG (SSS
postulate)
6. 
C is a right triangle (why?)
7. ABC is a right triangle (why?)
So when the Egyptians formed a triangle with equally spaced knots as described above, they did form a right triangle!
The triangle with sides 3 units,4 units, 5 units forms a right triangle
since . Any triple of integers such that is
called a Pythagorean triple. It is called a primitive Pythagorean
triple if 1 is the only common factor to all three integers.
Tests for Acute, Obtuse or Right Triangles:
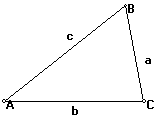
In triangle ABC, if c is the longest side
of the triangle, then
Relations of sides |
Type of Triangle |
|
Acute |
|
Right |
|
Obtuse |
Example: Determine if the triangles with the following sides are acute,right, or obtuse:
a. 9,40,41 |
b. 6,7,8 |
| Solution: | Solution |
The longest side is 41, so we will comare
So our triangle is right. |
The longest side is 8, so we will compare
So our triangle is acute. |
Click the lightbulb
to practice this lesson
with 
.
with
.
