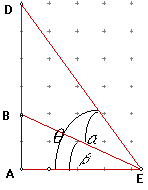
The Problem: A 4 by 4 picture hangs on a wall 2 ft. above your eye level. How far back from the picture should you stand in order to view the picture with maximum angle. You are standing directly in front of the picture. Below is a graphical representation of the problem as a side view.
We are trying to find the distance from A to E that maximizes 
.
To see howchanges as the length of AE changes:
Click Here to move E horizontally.
What we are asked to find is the distance in front of the mirror that
gives us a maximum .
If we look at out picture we can write an equation for as
a function of the distance in front of the mirror. We will call the distance
.
Since DAE is a 90 degree angle we have:
and
. The angle we are interested in is
, but we can see
=
, so we have:
=
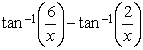. We can look at the plot of versus :
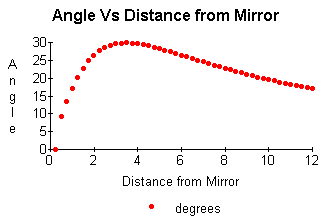
We see that when is maximum our tangent line to the
above curve would have slope of zero. Recall the slope of a tangent line
to a curve is found by taking the derivative of the curve with respect to
the independent variable, in our case since is varying. We must then remember, or look up, the derivative of the
inverse tangent function:
. Now we can find that gives us a maximum by setting the slope of the
tangent line of
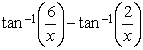
equal to zero. We get:
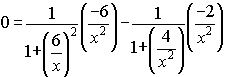
Simplifying:
.
Cross multiplying and simplifying we get:
,
so
.
Therefore 
, but since we are looking for a distance
we have
.
Does this agree with what we expected when looking at the picture?