Consider the general equation of a parabola:
We know that the graph of a quadratic will give us a parabola. How will changing a,b, and c affect the vertex of the parabola?
First let's look at the standard form for the equation of a parabola:
The vertex in the above form is at (h,k). We can put the general equation in terms of a,b, and c in the standard form by completing the square:
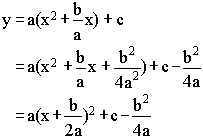
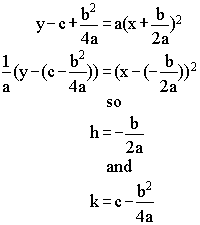
As we can see b and a will affect the x coordinate of the vertex, while a,b,and c all affect the y coordinate.
Now let's look at some graphs: First we will let b=0,c=0. From the solutions for h and k we expect the vertex to be at (0,0).
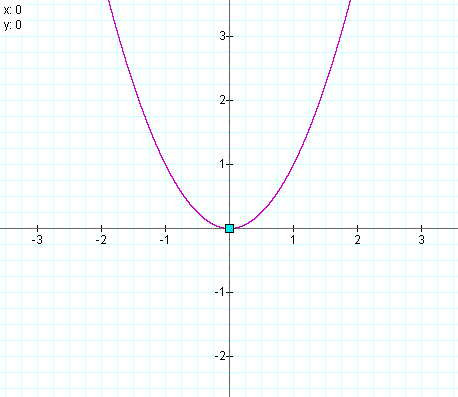
We know that with b and c equal to zero our vertex will be at (0,0), so what affect will changing a have on the parabola? Lets change a and look at the graphs:
The purple graph is a=.25,the red a=.5,the blue a=.75,the green a=1 and the aqua a=1.5. So we see as a increases the parabola gets thinner. If we look at the negatives for the previous values of a we get:
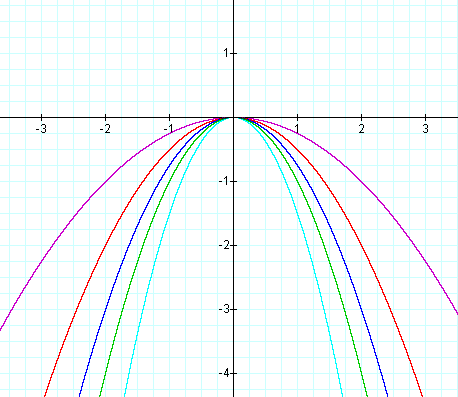
So negative values of a cause the parabolas to open downwards.
Remember the coordinates of the vertex in terms of a,b,c
where are:
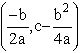
So let a=1 and b = 0. As we change c we expect the y coordinate of the vertex to change. As c increases the vertex will get higher. Lets look at a few parabolas:
The purple parabola was obtained when c = 0, the red when c = 1 and the blue when c = - 1.
Next we will look at the cases when a=1, c=0 and b
varies. The coordinates of the vertex will be: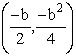
when we
plot these as x,y coordinates with b varying we get:
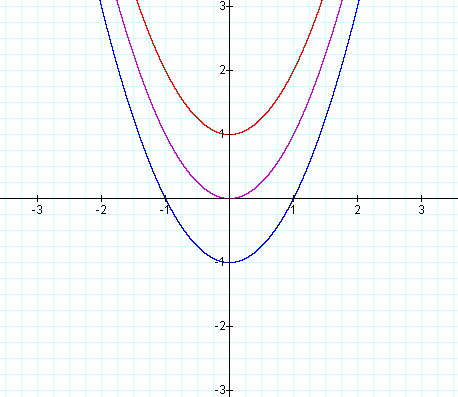
This is the locus of vertices for a=1 and c=0 with b varying. If we look at several parabolas on top of the locus of vertices we see:
red:b = 0,blue:b = 1,green:b = -1,aqua:b = 2,yellow:b=-2,lavender:b = 3,and,gray:b = -3:
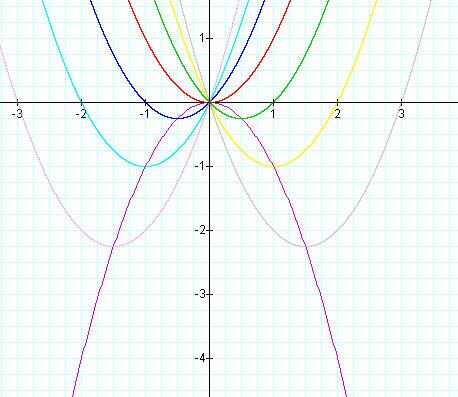
Now if we keep a=1 and vary c and b the coordinates of our vertex would be:
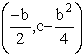
This will shift our parabola up by the constant c. If we look at the previous graph with c= 1, instead of zero, we get:
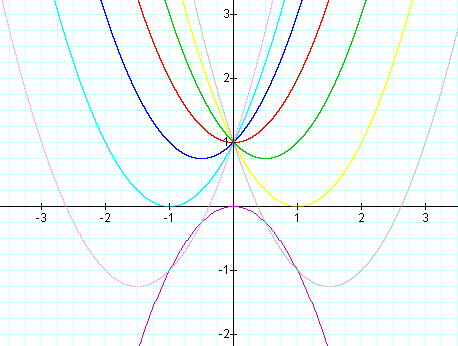
Our locus of vertices is now not correct. If we move it up 1 unit will it be correct?
Now for for c = -1 we would expect to shift the family of parabolas with b varying and a = 1 down one:
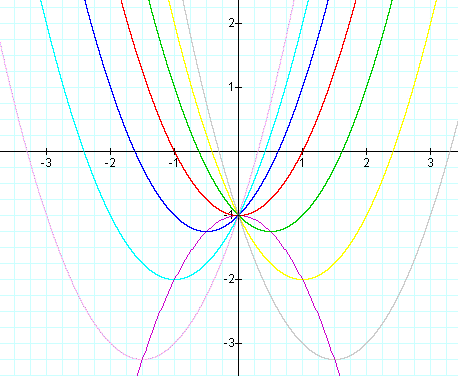
Now what happens when we vary a? Lets look at the values of the coordinates of the vertex in terms of the coefficients of our quadratic:
.
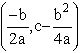As we can see changing a will affect both the x and y-coordinates of the vertex. Lets look at the family of parabolas with b varying and c=0 with different values of a. First with a=2 we will get the following:
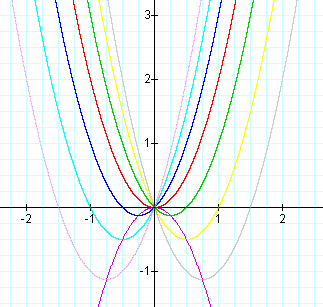
We can compare this to the graphs when a=1,c=0:
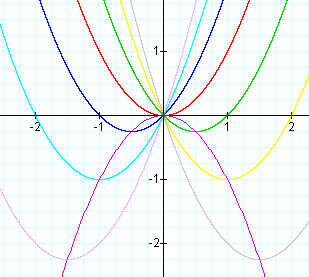
The equation of the vertex in the first graph with a=2,c=0
is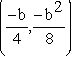
and for the second graph with a=1,c=0
the equation of the vertex is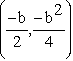 
. So we see that the
parabola with a=2,c=0 has a vertex with coordinates that are
one-half the coordinates of the vertex when a=1,c=0.
We looked at the graphs of as
we changed a,b,c. We saw changing a with b,c,constant we changed the
width of our parabola. As we let a go to zero
our parabola increased in width. For a positive a the
parabola opened upwards
and and a negative a caused our parabola to open downwards. We saw that changing c caused a vertical shift upwards
of the vertex by the value c and downwards the value c for negative c.
When we changed b
with a and c constant we found that the locus of vertices of our parabola was a parabola
itself.
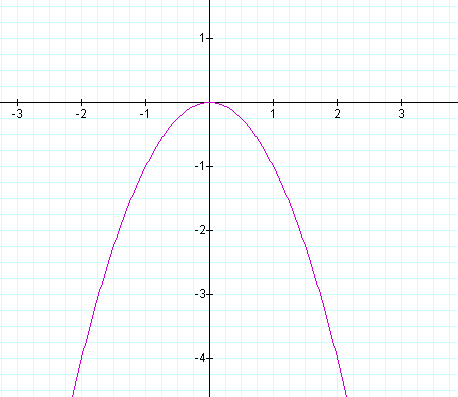
We saw the locus of vertices of our parabola
given by, ,
with a positive and b varying was a parabola that opened downwards. What affect would a negative a have on the locus of vertices parabola?
Recall the standard form of a parabola:.
When we put our equation ,, in standard
form we got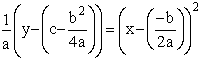 
.
We see that 
. If y =
k-p is the equation of the directrix of the standard parabola and the focus
is at (h,k+p) how does a,b,c affect the directrix and focus?
Links to Related Web Sites: