EMAT 6680 Assignment 3

It has now become a rather standard exercise, with available technology, to construct graphs to consider the equation

and to overlay several graphs of

for different values of a, b, or c as the other two are held constant. From these graphs discussion of the patterns for the roots of

can be followed. For example, if we set

for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following picture is obtained.

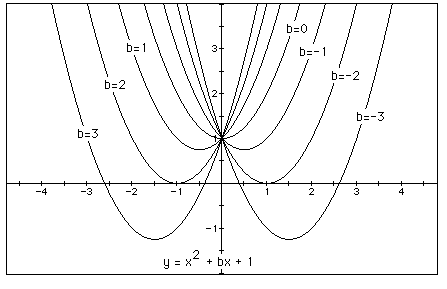
We can discuss the "movement" of a parabola as b is changed. The parabola always passes through the same point on the y-axis ( the point (0,1) with this equation). For b < -2 the parabola will intersect the x-axis in two points with positive x values (i.e. the original equation will have two real roots, both positive). For b = -2, the parabola is tangent to the x-axis and so the original equation has one real and positive root at the point of tangency. For -2 < b < 2, the parabola does not intersect the x-axis -- the original equation has no real roots. Similarly for b = 2 the parabola is tangent to the x-axis (one real negative root) and for b > 2, the parabola intersects the x-axis twice to show two negative real roots for each b.

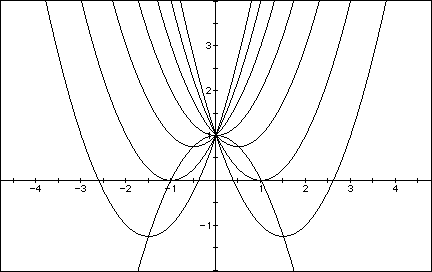
Now consider the locus of the vertices of the set of parabolas graphed from

Show that the locus is the parabola

Click Here for generalization to the locus of vertices of a parabola.

Graphs in the xb plane.

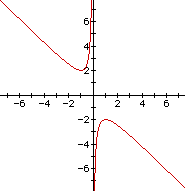
Consider again the equation

Now graph this relation in the xb plane. We get the following graph.

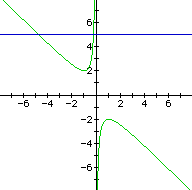
If we take any particular value of b, say b = 3, and overlay this equation on the graph we add a line parallel to the x-axis. If it intersects the curve in the xb plane the intersection points correspond to the roots of the original equation for that value of b. We have the following graph.

For each value of b we select, we get a horizontal line. It is clear on a single graph that we get two negative real roots of the original equation when b > 2, one negative real root when b = 2, no real roots for -2 < b < 2, One positive real root when b = -2, and two positive real roots when b < -2.

Consider the case when c = - 1 rather than + 1.

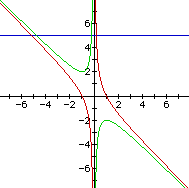
We can see for c=-1 any value of b will give us a root to our original quadratic equation. We can also see that one root will be positive, while the other is negative.

Now consider different values for c. The following equations were graphed:

to give the following graph:

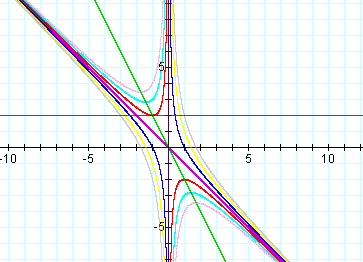
As we can see the line 2x+b=0 goes through the vertices for c > 0. Notice for b,c > 0 there are no real roots for b below this vertex. For b < 0 ,c > 0 there would be no real roots above this value. This occurs when .

Recall our original equation: when we get .

Therefore for c > 0 we will have two real roots for . We also can see from the graph that for a negative c we will always have two real roots for any value of b. For negative values of c would be satisfied for any value of b.

This gives us a graphical interpretation of the discriminant of the quadratic formula when a=1.

Graphs in the xc plane.

In the following example the equation

is considered. If the equation is graphed in the xc plane, it is easy to see that the curve will be a parabola. For each value of c considered, its graph will be a line crossing the parabola in 0, 1, or 2 points -- the intersections being at the roots of the original equation at that value of c. In the graph, the graph of c = 1 is shown. The equation

will have two negative roots -- approximately -0.2 and -4.8.

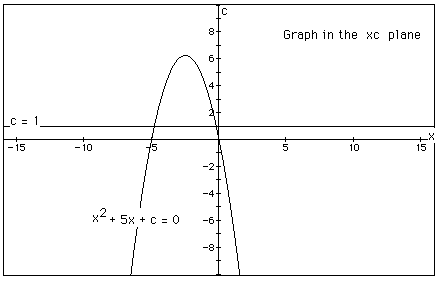
There is one value of c where the equation will have only 1 real root -- at c = 6.25. For c > 6.25 the equation will have no real roots and for c < 6.25 the equation will have two roots, both negative for 0 < c < 6.25, one negative and one 0 when c = 0 and one negative and one positive when c < 0.

What significance does c=6.25 have? How is it related to b?

In this equation b=5. Notice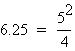 or .

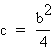Let us consider several graphs in the x-c plane:

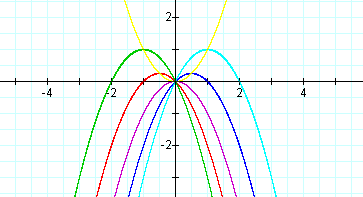
The locus of vertices is the yellow line and has the equation .

By graphing the equation in the x-b and x-c planes we were able to determine a relationship between the values of b and c that would give us a real solution. It is gives us a graphical interpretation of the discriminant (for a=1).

How would changing a affect our graphs in the x-b and x-c planes?

Return to Cathryn Brooks: Return

Send e-mail to jwilson@coe.uga.edu