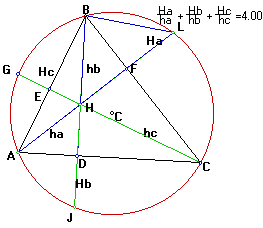
Consider an acute triangle ABC. Construct the altitudes of the triangle as rays and construct the circumcircle of ABC Let ha,hb,hc be the altitudes from vertex A,B,C respectively. Let Ha be the segment from vertex A to the point where the altitude meets the circumcirle. Similarly Hb and Hc are the segments of the altitude from the vertex to the intersection of the circumcircle :

Notice we have : ![]() . This is true for
all acute triangles ABC.
. This is true for
all acute triangles ABC.
Proof:
First Consider the two triangles: BHF and BFL. Angles BHL and BFL are congruent since the both subtend the same chord on the circumcircle. BFH and BFL are both 90 degrees since AF is an altitude. They share the side BF. Therefore they are congruent so HF = FL. Similarly HE = EG, HD = DJ. So we have the following:
![]()
![]() and
and ![]() .
.
Now we have
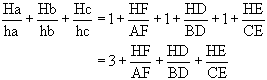 .
.
Now let's consider ![]() .
First look at the triangle again:
.
First look at the triangle again: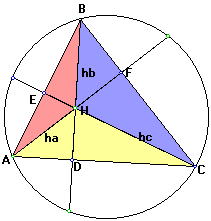
We see that BD*AC is two times the area of ABC since BD is the height for the base AC. CE*AB and AF*BC are also 2 times the area of ABC. We will call this number X. Now notice that the area of ABC could be computed by summing the areas of BHC,AHC, and AHB since they cover the same area. Then 2 times the area of BHC is HF*BC, the area of AHC is HD*AC and the area of AHB is EH*AB. So Now consider again:
![]()
Now notice the values in the denominators of the ratios on the right-hand side of the above equation. The are all two times the area of ABC or X. We can factor this out:
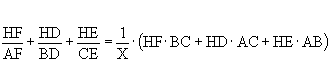
But ![]() , so we have
, so we have![]() .
Therefore
.
Therefore
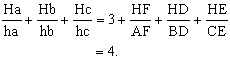
Note: The key to this proof was to use the areas - Thanks to Dr. J. Wilson!