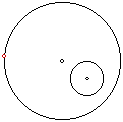

As I began this assignment I began to notice that it was quite easy to construct one tangent circle for two circles. A step by step procedure can be found on the assignment page located at: http://jwilson.coe.uga.edu/EMT668/Asmt7/EMT668.Assign7.html. The following write up will look at what happens to the locus of the center of the tangent circle when the designated point moves around the given circle.
First, let's look at when
one circle lies completely within the other circle and let the point be
designated on the larger of the two circles.
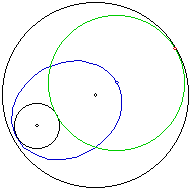 The green circle is the tangent circle to the two black circles.
The locus of this circle can be seen in blue. Here we notice that the locus is an ellipse. It appears
that the foci of this ellipse would be the centers of the first two circles.
This would make perfect sense through a few steps of reasoning. First a
circle is all the points that are equidistant around one point. Thus we
have to sets of points that are equidistant around two distinctively different
points. Thus when I create a circle that is tangent to both of the circles,
the center will be equidistant from the two centers of the circles, allowing
the locus created to be an ellipse.
The green circle is the tangent circle to the two black circles.
The locus of this circle can be seen in blue. Here we notice that the locus is an ellipse. It appears
that the foci of this ellipse would be the centers of the first two circles.
This would make perfect sense through a few steps of reasoning. First a
circle is all the points that are equidistant around one point. Thus we
have to sets of points that are equidistant around two distinctively different
points. Thus when I create a circle that is tangent to both of the circles,
the center will be equidistant from the two centers of the circles, allowing
the locus created to be an ellipse.
Next, let's look at the same
two circles but let the designated point be on the smaller of the two circles.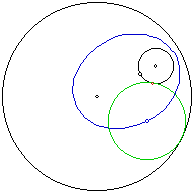
Notice that once again we get an ellipse.
Thus we can conclude when we have two circles, one lying within the other, then the locus of the center of the tangent circle (when the designated point moves around the circle) is an ellipse.
Also note that the designated point is in red.
What if the two circles lie
completely seperate from each other? In other words, one is on one side
of the paper and the other is on the other side of the paper. Look at the
following picture.
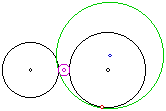
We see that not only do we have the green tangent circle through the designated point but that there is another tangent cirlce between the two circles. This is designated by the purple circle. We are still interested in the locus of the center of the green circle.
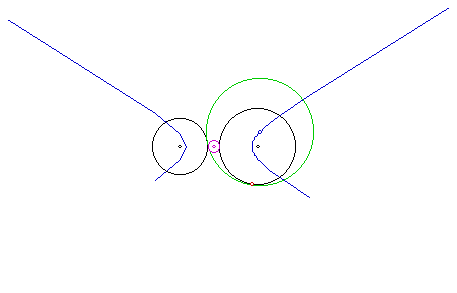
Notice that instead of an ellipse we now have a hyperbola. Once again it appears that the centers of the two original circles are the foci of the two "parabolas".
 After looking at many various examples, I have found
that when two circles are independent of each other, the locus of the tangent
circle (constructed from a designated point) is a hyperbola.
After looking at many various examples, I have found
that when two circles are independent of each other, the locus of the tangent
circle (constructed from a designated point) is a hyperbola.
Finally let us look at when the two circles intersect. We
see that once again there are two tangent circles. We will be looking at
the locus of the center of the green circle.

We can see that once again we have an ellipse.
Click here for the GSP sketch that allows
you to investigate these circles on your own.