

The probability of an event is a number describing the chance that the event will happen. An event that is certain to happen has a probability of 1. An event that cannot possibly happen has a probability of zero. If there is a chance that an event will happen, then its probability is between zero and 1.
Examples of Events:


Events that are certain:
Events that are uncertain:
Let's take a closer look at tossing the coin. When you toss a coin, there are two possible outcomes, "heads" or "tails."
Examples of outcomes:
The set of all possible outcomes of an experiment
is the sample space
for the experiment.
The two outcomes of tossing a coin are equally likely, which means that each has the same chance of happening. When all outcomes of an event are equally likely, the probability that the event will happen is given by the ration below.
![]()
When looking at the probability of the event that the coin lands on tail we get the following:


These events are equally likely to happen:
When the outcome of one event does not affect the outcome
of a second event, the events are independent. When the outcome of one event does affect the outcome of the
second event, the events are dependent. Let's look at the following five examples. Decide which pair
of events are dependent or independent. 
1. Toss a coin. Then roll a number cube (die).
2. Choose a bracelet and put it on. Choose another bracelet.
3. Select a card. Do not replace it. Then select another card.
4. Select a card. Replace it. Select another card.
5. Pick one flower from a garden, then pick another.
The events above that are independent are numbers 1 and 4.
Probability of Two Independent Events
![]()
Given a coin and a die, what is the probability of tossing a head and rolling a 5?
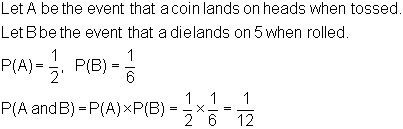
The events above that are dependent events are numbers 2, 3, and 5.
Probability of Two Dependent Events
![]()
Given a deck of cards, what is the probability that the second card drawn will be from the same suit if the first card drawn is the Queen of Hearts?
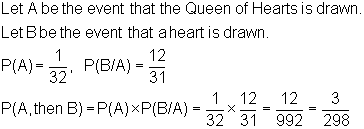

The
Counting Principle
The number of outcomes of an event is the product of the number of outcomes for each stage of the event.
Let's suppose that we want to find out how many different license plates are possible, when the license plate is composed of three digits then three letters. To do this you can use the counting principle. The product below gives the number of different plates possible.
![]()
![]()
We can use this same principle even if there are stipulations on the problem. For example say that a number or letter can only be used once.
![]()
What if we wanted to know which plate system provided more possible outcomes, one with five letters or one with seven digits?
Five letters: |
Seven digits: |
So we see by using the counting principle that there are
more possibilities if we use five letters instead of seven digits.