

The purpose of this paper is to convey a creative method for discovering and teaching ellipses and hyperbolas. Circles, ellipses, and hyperbolas are all conic sections, so when the student understands circles it is logical to use circle constructions to form ellipses and hyperbolas.
Conic Section Overview:
Two double right cylinder cones are shown below. Each cone consists of all lines, or elements, through point V that form a given angle with line a. Point V is called the vertex of the cone, and line a is the axis. Curves like ellipses and hyperbolas formed by the intersection of a plane and a cone of this type are called conic sections or conics.
Ellipses
If a plane is tilted in such a way that its intersection with a right circular cone is a closed curve, then that intersection is an ellipse. An ellipse is the set of all points P in a plane such that the sum of the distances from P to two fixed points is a constant. Each of the fixed points is called a focus. A common method of teaching ellipses is to fix two points, say two nails on a board, and use a piece of string tied loosely between the points to demonstrate how ellipses are drawn as indicated by the picture below. Pulling the string tightly with a pencil and tracing in a circular motion will produce an ellipse.
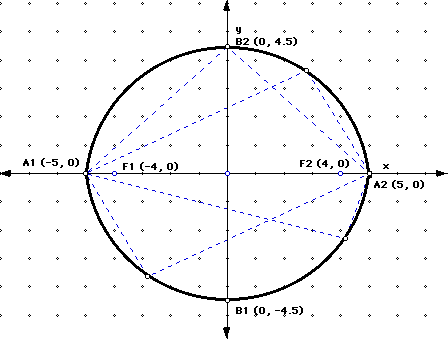
Line segment A1A2, which contains the foci, is the major axis of the ellipse. The shorter segment B1B2 is the minor axis. The midpoint of F1F2 is the center of the ellipse, and for this ellipse, the center is the origin. Note the relationship among the squares of the intercept and the square of the distance from a focus to the center.
The standard form of the equation of an ellipse centered at the origin is:
If a > b the major axis is along the x- axis, but if a < b the major axis is along the y-axis.
Our method of discovering ellipses begins with an investigation of tangent circles. Specifically, given two circles and a point on one of the circles, construct a circle tangent to the two circles with the given point as the point of tangency.
In the following example the given point is on the larger circle.
Click here to run a GSP script for the construction as indicated below. You can also click here to further investigate the actual GSP picture.
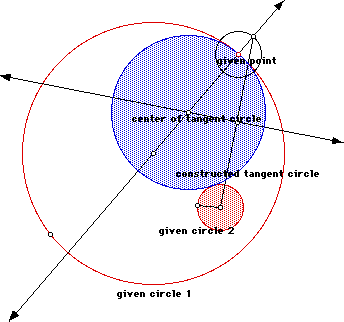
The above circle (as the GSP script will dictate) was drawn by constructing a line through the center of the larger circle with the designated point of tangency and then constructing a circle of the same radius as the smaller circle with the designated point as center. The intersection of the line and circle will allow construction of the base of the isoceles triangle and hence allow location of the center of the desired circle.
Now construct the tangent circle to the two given circles if the given point is on the smaller of the two circles so that the smaller circle is external to the tangent circle. For a GSP script click here. Additionally, click here to manipulate the GSP sketch below.
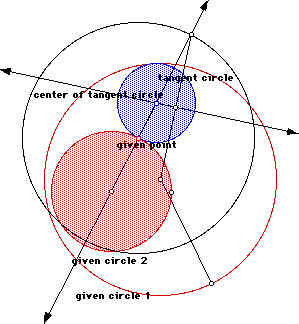
Considering the locus of the center of the circle tangent to the given circles, we can animate the given point around given circle 2 and trace the center of the tangent (blue) circle as shown below to form an ellipse. Click here to see and manipulate a GSP picture to construct an ellipse using this method.
Hyperbolas:
If the intersection of a plane and a double right cylindrical cone (shown above) contains points in both the top and the bottom of the cone (excluding the vertex), that intersection is called a hyperbola. Thus, a hyperbola is the set of points P in a plane such that the difference of the distances from P to two fixed points is a constant. As in the case of the ellipse, the two fixed points are called foci.
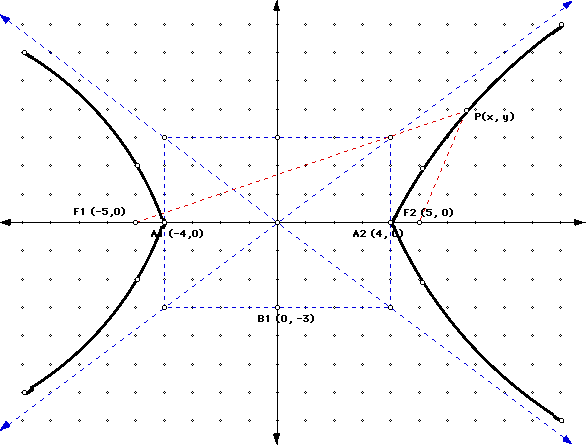
Let P(x, y) be an arbitrary point on a hyperbola with foci F1 (-5, 0) and F2 (5,0) and with the difference between the distances PF1 and PF2 equal to 8.
The hyperbola as shown above has two parts or branches. Line A1A2 contains
the foci, and segment A1A2 is called the transverse axis of the hyperbola.
Segment B1B2 is the conjugate axis. The center of the hyperbola is the midpoint
of F1F2, which in this case, is the origin. Note the relationship among
the coordinates of the endpoints of the transverse and conjugate axes and
the coordinates of the foci: 52 = 42 + 32.
Lines perpendicular to the coordinate axes at (4, 0), (-4, 0), (0, 3), and
(0, -3) form a rectangle whose extended diagonals are the asymptotes of
the hyperbola. The hyperbola never meets its asymptotes, but approaches
them more and more closely as |x| and |y| increase. The slope of one diagonal
in the above diagram is 3/4 and the slope of the other is -3/4, so the equations
of the asymptotes can be written y = 3/4x and y = -3/4x. A hyperbola may
have its foci on the y-axis, in which case the transverse axis is vertical.
The equations for hyperbolas centered at the origin, and with foci on a
coordinate axis, are ![]() when
the transverse axis is on the x-axis, and
when
the transverse axis is on the x-axis, and ![]() when
the transverse axis is on the y-axis.
when
the transverse axis is on the y-axis.
To use GSP to construct a hyperbola, construct the tangent circles as depicted above, however, this time construct them so that the given point is on the smaller of the two circles and the smaller circle is internal to the tangent circle as depicted below. Click here to run a GSP script for the construction, and click here to manipulate a GSP picture as shown below.
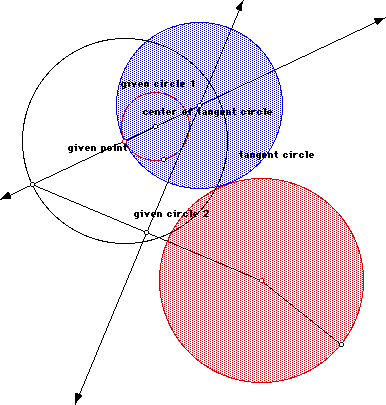
Considering the locus of the center of the circle tangent to the given circles, we can animate the given point around given circle 1 and trace the center of the tangent (blue) circle as shown below to form a hyperbola. Click here to see and manipulate a GSP picture to construct a hyperbola using this method.
Conic sections, specifically ellipses and hyperbolas, are evident and are used in everyday life. For example, the planets revolve around the sun in an elliptical orbit, with the sun at one focus. Other examples of elliptical orbits are satellites orbiting the sun and electrons orbiting the nucleus of an atom. Properties of a hyperbola are also used in navigation. An aircraft can determine the difference in its distance from two fixed transmitters by measuring the difference in reception times of synchronized radio signals. This puts its path on a hyperbola, with the two transmitters serving as foci. If another pair of transmitters are used, the aircraft must lie at the intersection of the two corresponding hyperbolas. The navigational system, LORAN, is a system of long-range navigation that is based on this principle.