Objective: Students will be able to find the probability of independent and dependent events.
Have you ever been asked to play a game that
involved tossing a coin, rolling a die, or even throwing objects
at a specified target? Did you ever think about whether or not
the game was fair?
In order to determine the fairness of a game we need to examine
some aspects of probability.
Probability is the likeliness of some event occurring. For example, what is the probability of flipping
and coin and landing with heads up?
In order to answer this question, we must examine the sample
space or the set of all possible outcomes of the toss. In
our coin experiment, the sample space includes only two elements--heads
and tails. The toss itself is called the event.

The probability of an event is determined by dividing the number
of successes by the total number of outcomes in the sample space.
A coin has one (1) head and one (1) tail. If I desire a head on
my coin toss and it occurs, that is called a success. There is
one head and two possible outcomes in the sample space.
The notation of this probability would be written as P(Heads)=
1/2 or .5.
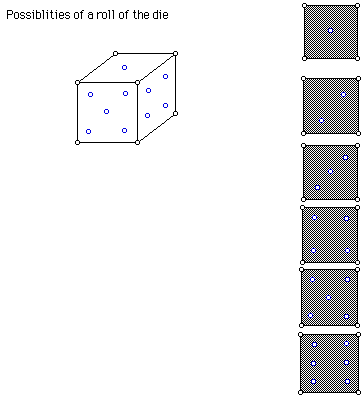
Above is a picture of a die. To the right are all of the possible outcomes of the roll of one die. Suppose you were asked the probability of rolling a 5. There is only one side of the die that contains a 5 but there are 6 possible outcomes. Therefore the probability of rolling a 5 is 1/6. Mathematically this could be written as P(5)=1/6.
What would be the probability of rolling a prime number?
Practice problems - Set One:
Use these problems to determine your
understanding of the material.
1. What is the probability of throwing a six (6) on one roll of
a die?
2. Find P(even number) on one roll of a die.
3. Find P(Tails) on one toss of a coin.
4. Using a "funny die" with sides numbered
{1,2,3,4,4,5}, Find P(1), P(2), P(3), P(4), P(5).
5. A coin has been tossed 10 times and has come
up heads each time. What is the probability that it will land
on heads on the eleventh toss?
GO TO ANSWERS
What is the probability of rolling a seven (7) on a regular six-sided
die?
Well since there is no seven on the die, it would be impossible
to have such a result. The probability of the event that is impossible
is zero (0).
What is the probability of a coin landing on heads
or tails when tossed? Since that must occur unless the
coin is weighted or tampered with to make it stand on its side,
we call that probability a certainty. The probability of an event
that is a certainty is one (1).
Based on the probability of an impossible event and the probability
of a certain event (these being the extremes), the probability
of an event can be expressed as a number between 0 and 1.
Referring back to a regular coin, find the sum of the probabilities
P(Heads) and P(Tails).
Examine the probabilities for a die.
P(1) + P(2) + P(3) + P(4) + P(5) + P(6) =
1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 6/6 = 1
This looks like a pattern. Find the sum of the probabilities of
the funny die in the practice problems.
P(1) + P(2) + P(3) + P(4) + P(5) = 1/6 + 1/6 + 1/6 + 2/6 + 1/6
= 6/6 = 1
Sums of probabilities are also used when two events
occur that have no elements in common. The sum of the probabilities
of independent events (no elements in common) is one (1).
For example, Suppose you roll a standard die.
The probability of getting an even number is the sum of the probability
of getting a 2, plus the probability of getting a 4, plus the
probability of getting a 6.
Practice Problems - Set Two.
A card is selected at random from a deck of 52
cards.
1. What is the probability of selecting a black
card?
2. What is the probability of selecting a queen?
3. What is the probability of selecting a one
(1)?
4. What is the probability of getting a face card?
5. Find the sum P(Hearts) + P(Clubs) + P(Diamonds)
+ P(Spades) =
Go to Answers
It is now time to simulate a game. Given two die (dice), roll
the dice. If the dice land on the same number, give yourself a
point. If the dice lands on different numbers, give the computer(ME)
a point.
Continue this game for approximately two minutes and collect your
results on a sheet of paper.
Do you think the game is fair? Before we give
the answer to this question, let's look at your results.
Using the results of your simulation, you can
write a fraction that represents your results. Using simulations
to find the number of times a desired outcome occurs is called
experimental probability.
P(Match) = the number of times the dice matched
/ the total number of rolls.
Below is a list of all of the possible outcomes
when the dice are rolled.
1-1, 1-2, 1-3, 1-4, 1-5, 1-6, 2-1, 2-2, 2-3, 2-4, 2-5, 2-6, 3-1,
3-2, 3-3, 3-4, 3-5, 3-6, 4-1, 4-2, 4-3, 4-4, 4-5, 4-6, 5-1, 5-2,
5-3, 5-4, 5-5, 5-6, 6-1, 6-2, 6-3, 6-4, 6-5, and 6-6.
How many total outcomes are there?
How many are matches?
How many are no matches?
Using the results from our list of all possible
outcomes to determine the probabilities is called theoretical
probability.
The probability of a match in our game of dice
is 6/36.
The probability of no match in our game of dice is 30/36.
The game you just played was not fair. The probability of no match
was much greater than the probability of a match. The computer
was sure to win.
What makes a game fair? Most of you would agree that a game is
fair if each participant has an equal chance to win.
Expected Value is
used to determine the fairness of a game. The sum of the products
of the outcome and its probability is called the expected value.
Suppose we had a 12-sided die, called a dodecahedron, whose faces
were marked in this fashion: 3, 3, 2, 2, 2, 2, 0, -1, -1, -1,
-1, -4. In the game, you are awarded the number of points on the
face of the die. Would this game be a game that could be won?
If we set up a table of the possible outcomes and their probabilities,
we have
In playing the game, the result of the expected
value determines winnings and losses. A positive expected value
represents wins and a negative expected value represents losses.
The above game gave a positive expected value which means over
a period of time you would have points.
Let's return to our previous question. What makes a game fair?
Although we stated that each player should have an equal chance
to win, how would that be expressed mathematically?
If two players were playing a game, if one had a positive expected
value and the other had a negative expected value, would we think
that the game was fair?
In order for the players to have an equal chance against each
other or the game itself, the expected value must equal zero (0).
Examine another game that involves money.
A game is played with these rules.
A player wins $3 if he draws an ace, $2 if he draws a king, and
$0.50 if he draws a queen or jack.
A player must pay the "kitty" $0.50 if he draws a 10,
9, or 8 and $0.75 if he draws a 7, 6, 5, 4, 3, or 2.
Is it a fair game for the player?
x ----- Ace ----- King ----- Queen/Jack -----10,9,8---7,6,5,4,3,2
P(x) -- 4/52 --- 4/52 ---------8/52 ----------- 12/52--------
24/52
---------1/13 ----1/13 ---------2/13 ----------- 3/13 ---------
6/13
Because the expected value is 0, the game is fair,
if the player so chooses to play. Does this mean the player will
win? Not necessarily. Actually, if the player plays long enough,
the amount that should be won would be 0. The expected value or
probability may not happen with just a couple of games.
Practice Problems-Set 3
1. If you toss a regular die and double the number on the
face of the die, find the expected value.
2. Find the expected value if you toss a regular
die and subtract one from the square of the number on the face
of the die.
3. Suppose you have six coins in your pocket:
a penny, a nickel, two dimes, and two quarters. What is the expected
value when you pull out one coin?
4. Many people play roulette when visiting Las
Vegas. A mechanical wheel contains numbers from 1 to 38. The device
randomly selects one of 38 equally likely numbers. If a player
chooses one particular number, suppose he gains $35 if his number
is selected, but losses $1 if it is not. Calculate the expected
value of the game.
5. The 38 numbers in a roulette wheel are colored:
18 red, 18 black and 2 white. If a player chooses a color, he
wins a $1 if a number of that color is selected; if not, he losses
$1. Is the game fair?
Go to Answers
The above questions were taken from
Introductory Statistics and Probability, A Basis for Decision
Making by David W. Blakeslee and William G. Chinn, Houghton Mifflin
Company, 1975.
Probabilities of Compound Events
If a student has three skirts to wear to school:
1 blue, 1 black, and 1 plaid. She has four blouses: 1 white, 1
red, 1 green and 1 with pink flowers. What is the probability
that if she dressed in the dark (choosing her outfit at random),
she would wear the plaid skirt with the blouse with pink flowers?
First we will make a tree diagram to view the
different outfits possible.
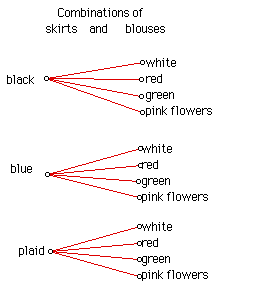
There are 12 possible outfits for the student
to wear. There is only one successful outcome on the tree diagram.
Therefore the P(plaid skirt, pink flower blouse) = 1/12.
There is another way to solve this problem without using a tree
diagram. In probabilities involving multiple events where the
events are independent of each other use the following:
Use the above rule to answer the following
question.
In a game, a player is to flip a coin and roll a die. What is
the probability of heads on the coin toss and a 6 on the roll
of the die?
Notice the toss of the coin has nothing to
do with the roll of the die. These are independent events.
If the result of a second event is altered by the event that occurred
in the first event, the events are dependent.
The best example of dependent events can be found
using a standard deck of cards. Suppose two cards are dealt from
a standard deck without replacing the first card drawn. Consider
the probabilities of the following:
There are 52 cards at the beginning of the
compound event. Half of the cards are red, so the probability
of a red card on the first draw is 26/52. Once that card is drawn,
regardless of the color, the number of cards to select from has
changed. There are now only 51 cards.
When discussing the probability of a compound
event it is important that we assume the first event is successful.
If the first event is unsuccessful, it would be useless to continue
the compound event.
Therefore in our first draw, we assume a red card
was drawn. In that case, there are only 25 red cards remaining,
so the probability of a red card on the second draw is 25/51.
Find the probability
Again, the draw begins with 4 aces and 52 total
cards.
P(first card is not an ace and second card is
not an ace)=
P(first card is not an ace) * P(second is not an ace/given that
the first card was not an ace)
P(neither card is an ace) = (48/52) * (47/51) = 188/221
Practice Problems Set 4
1. Using a standard deck of cards, what is the probability
of drawing two cards from the deck without replacing the first
card drawn, that the cards will be an Ace and a king?
2. What is the probability of drawing three cards
without replacement so that all of the cards will be face cards?
Go to Answers
Return
to Introduction