
Objectives:
Students will be able to
1) define polygonal region
2) find the perimeter of a polygon
3) determine the area of parallelograms (including the rectangle, rhombus, and square), triangles, trapezoids, and regular polygons.
Below are the terms associated with finding area and perimeter.
A polygon is a plane figure whose sides are three or more coplanar segments that intersect only at their endpoints. Consecutive sides cannot be collinear and no more than two sides can meet at any one vertex.
A polygonal region is defined as a polygon and its interior.
The perimeter of a polygon is the distance around the figure. The area of a polygonal region is measured in square units. For every polygonal region, there is a unique positive number called the area of the region.
The area of a polygonal region is the sum of the areas of all its non overlapping parts. The area of a figure represents how many square units fit inside a figure without overlapping or leaving gaps. It is what's inside the sides like carpet on the floor. Area is always stated in square units.
In the example below, the area of the rectangle CDEF can be found by counting the number of square units inside the region. In the rectangle below, there are 18 square units of area within the figure.

Another way to find the area of a rectangle is to multiply the number of units of the base times the number of units of height, or simply Area = bh. In the above rectangle, the area would be calculated by multiplying 6 X 3 to get 18 square units. When figures are not placed on a grid like the example above other information can be given to help you find the area.
Below are formulas for the triangle and quadrilaterals that are used frequently in geometry. In each case, there must be an appropriate height that is perpendicular to the base.

Although the square is easily derived from the area of a rectangle formula, the others may not appear so straightforward in their relationship to the rectangle.
Take a look at the Geometer's Sketchpad 4.0 demonstration that shows the relationship between rectangles and the other figures shown above.
Journal opportunity #1: When you merged the point to the parallel line, what transformation did that illustrate? Explain the relationship between the area of a triangle and the area of a parallelogram.
AREA PRACTICE
Find the area of each figure below.
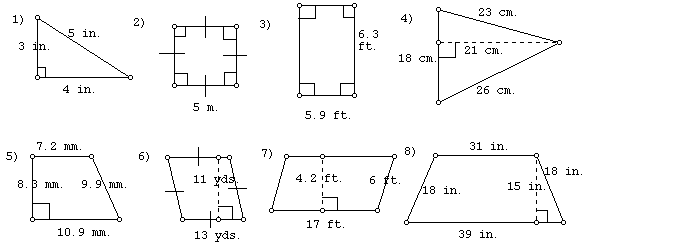
Click here to check your work.
Finding perimeter is simply finding the sum of the lengths of the sides. Perimeter represents the distance around a figure.
Find the perimeter of the following figures.
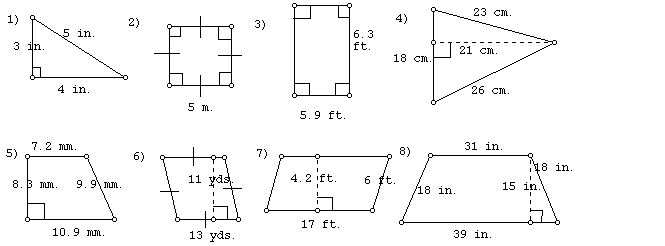
Click here to check your perimeters.
Some figures have shapes that are defined by the above formulas. They may be shaped in a combination of previously explored figures. If the figure can be divided into polygonal regions, like triangles, parallelograms or trapezoids, the area can be found by find the sum of these regions. It is important that these regions do not overlap or leave gaps. It is possible that several different formulas for area might be used to get a total area.
In order to find the area of irregular polygonal shapes, divide the shape into smaller regions of triangles, parallelograms, or trapezoids that do not overlap. Once the area of each region has been found, the sum of these regions will give the area of the entire figure. Below are some examples where the shape has already been divided.
Take a look at this GSP figure:
Area Practice for Various Polygonal Regions
Find the area of the following figures:

Click here to check your answers.
Another type of polygon and its region that can be explored is the regular polygon. A regular polygon is both equilateral and equiangular. The center of a regular polygon is the point of intersection of the perpendicular bisectors of the sides. The segment from a vertex to the center is the radius. The perpendicular segment from the center to a side is an apothem. The picture below illustrates these definitions.

The area of a regular polygon is one-half the product of its perimeter and its apothem, or A=(ap)/2. The picture below illustrates finding the area to an equilateral triangle:

Students should be able to find the area of various regular polygons if they have enough information about the figure, such as angles measures, length of the center, the radius, or the length of a side.
PRACTICE ON AREA OF REGULAR POLYGONS
From the given information, find the area of the regular polygons below.
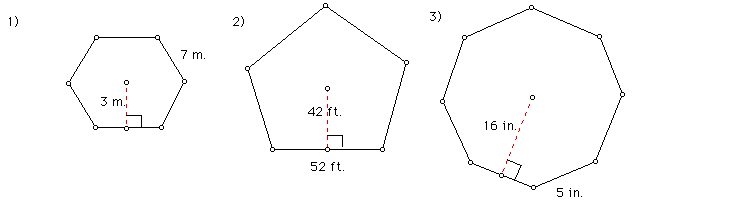
This concludes Lesson 1 on area. You should now be able to find the area of various types of geometric figures.
Return to Introduction