Assignment #6.9 & 10
Alternations to the Directrix of a Parabola
#1 Directrix as a line - The Parabola
A parabola is defined as all points equidistant from a
line, called the directrix, and a fixed point, called the focus.
 |
 |
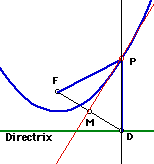
(Diagram Left) The locus of
the points equidistant from F (focus) and D (a point on the directrix) is
found at the point of intersection between the perpendicular bisector of
FD and the perpendicular line to the directrix through D.
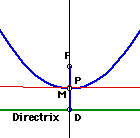
(Diagram Right) This is a special
case when the point equidistant form F (focus) and D (a point on the directrix)
is the midpoint of the perpendicular segment to the directrix through D.
 Use GSP to create the parabola. Click here if this didn't
work. Use GSP to create the parabola. Click here if this didn't
work.
|
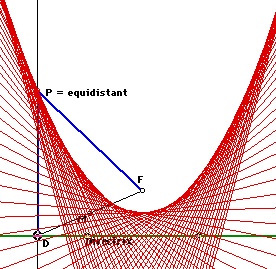
The locus on tangent lines to the parabola defines it shape
nicely.
 View the parabola defined
by its tangent lines. View the parabola defined
by its tangent lines. |
 |
#2 Directrix as a circle - Creation of the hyperbola
and ellipse
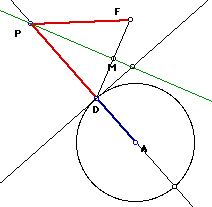 |
This is the basic configuration when the directrix
is circle. F is the focus point, D is the point on the directrix (the circle),
M is the midpoint of the line segment of FD, and P is the point of intersection
between the perpendicular bisector of FD and the perpendicular line to the
directrix though D.
This is the exact same setup as the parabola except D is
on a circle instead of a line.
|
Case #1 - F is outside the directrix (the circle)
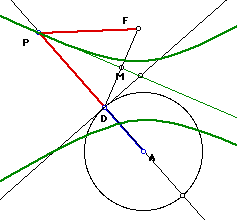 Looking at the diagram on the right we see the locus of
points (green lines) formed when F is outside the circle and D is moved
along the directrix (the circle). A hyperbola is formed when there is a
constant difference between the distances of the two focal points. This
is true for the diagram.. By construction FP = DP, these are the two equal
arms of the isoceles triangle. The length DA is a fixed amount in that it
represents the radius of the circle with center A. Thus the fixed difference
is found in PA - PF. This value is a constant amount because as PF expands
or shrinks, the corresponding equal arm PD which is apart of segment PA
will also expand or shrink an equal amount. Thus to summarize this particular
case, when F is outside the circle, a hyperbola formed between the foci
of F and A.
Looking at the diagram on the right we see the locus of
points (green lines) formed when F is outside the circle and D is moved
along the directrix (the circle). A hyperbola is formed when there is a
constant difference between the distances of the two focal points. This
is true for the diagram.. By construction FP = DP, these are the two equal
arms of the isoceles triangle. The length DA is a fixed amount in that it
represents the radius of the circle with center A. Thus the fixed difference
is found in PA - PF. This value is a constant amount because as PF expands
or shrinks, the corresponding equal arm PD which is apart of segment PA
will also expand or shrink an equal amount. Thus to summarize this particular
case, when F is outside the circle, a hyperbola formed between the foci
of F and A.
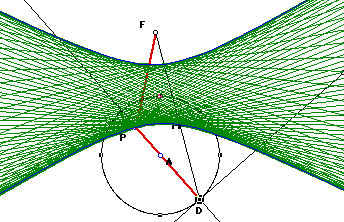
To view the creation of the hyperbola using the following
properties click on the following symbol.
Case #2 - F is inside the directrix (the circle)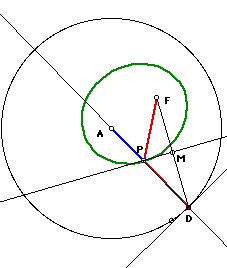
Looking at the diagram on the right we see the locus of
points (green lines) formed when F is inside the circle and D is moved along
the directrix (the circle). An ellipse is formed when the sum of the distances
from a point to the two focal points is held constant. This is true for
the diagram on the right. By construction FP = DP, these are the two equal
arms of the isoceles triangle. The length AP is the circles radius DA minus
the arm of the the isoceles DP. AP + FP is always a constant because they
must add up to the circles radius which of course does not change.. Thus
the fixed sum is found in AD. Thus to summarize this particular case,
when F is inside the circle, an ellipse formed between the foci of F and
A.
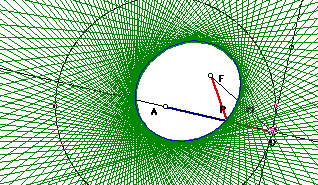
To view the creation of the ellipse using the following
properties click on the following symbol.
#3 Directrix as a line in motion (Further Investigation)
The directrix will be formed under the following
conditions:
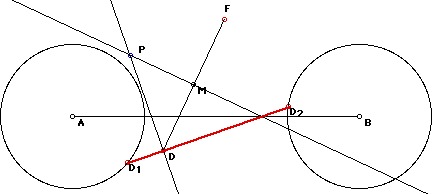 |
The directrix (red line) which we are referring to is the
line segment from D1 to D2. The line from D1 to D2 line will change size
and position as D1 and D2 move around their respective circles. The rest
of the points are similar to previous experiments F is the focus point,
M is the midpoint of DF, and P is the point equidistant from F and D.
Some things to explore are:
What shape is created? How is the shape altered as F moves
location? How is the shape altered if the two circles are different sizes?
What happens if only D1 moves along its circle while D2 remains constant? |
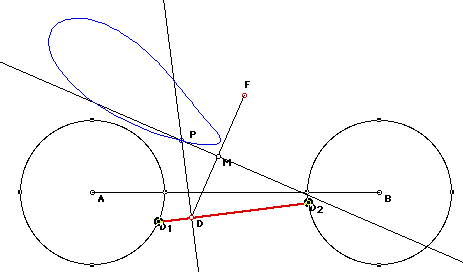 |
This is just one result of many but the locus of points
formed is somewhat of a skewed teardrop. Use the following script to begin
your own investigations.
I want to investigate. |
The end!!




 Looking at the diagram on the right we see the locus of
points (green lines) formed when F is outside the circle and D is moved
along the directrix (the circle). A hyperbola is formed when there is a
constant difference between the distances of the two focal points. This
is true for the diagram.. By construction FP = DP, these are the two equal
arms of the isoceles triangle. The length DA is a fixed amount in that it
represents the radius of the circle with center A. Thus the fixed difference
is found in PA - PF. This value is a constant amount because as PF expands
or shrinks, the corresponding equal arm PD which is apart of segment PA
will also expand or shrink an equal amount. Thus to summarize this particular
case, when F is outside the circle, a hyperbola formed between the foci
of F and A.
Looking at the diagram on the right we see the locus of
points (green lines) formed when F is outside the circle and D is moved
along the directrix (the circle). A hyperbola is formed when there is a
constant difference between the distances of the two focal points. This
is true for the diagram.. By construction FP = DP, these are the two equal
arms of the isoceles triangle. The length DA is a fixed amount in that it
represents the radius of the circle with center A. Thus the fixed difference
is found in PA - PF. This value is a constant amount because as PF expands
or shrinks, the corresponding equal arm PD which is apart of segment PA
will also expand or shrink an equal amount. Thus to summarize this particular
case, when F is outside the circle, a hyperbola formed between the foci
of F and A.



