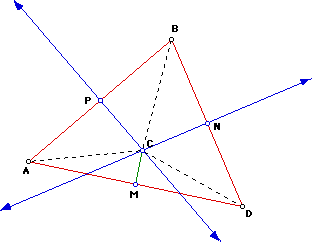

Let the perpendicular bisectors of AB and BD meet at C.
Construct a line segment from C to AD such that CM is perpendicular to AD.
Triangles APC and BPC are congruent (SAS) hence AC = BC, also
triangles BNC and DNC are congruent (SAS) hence BC = DC, and
hence AC = DC.
Therefore we can show that triangle AMC and DMC are congruent (RHS) and
hence AM = MD showing that line MC is the perpendicular bisector of side
AD.
From the discussion it is clear that AC = BC = DC and hence any circle with
C as center and passing through one of the vertices will pass thrtough all
of them.