INSTRUCTIONS:

Complete each of the following parts. Part One is merely finishing off the write-ups for the semester. Part Two should be new web page items. Part Three is the course evaluation.

Part One

Review your Write-ups 1 to 12. Revise as you wish to reach the point where you feel that, collectively, the 12 write-ups represent your best work for the course. They are an elctronic portofolio of your work.

Part Two

Complete a Write-up on your Web Page for each of the following investigations. This should be individual work.

A. Bouncing Barney. We discussed this investigation in class. Your challenge now is to prepare a write-up on it, exploring the underlying mathematics ideas and conjectures.

Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.

I assume some GSP sketches and explorations will be useful as well as proofs of the conjectures. A highly regarded write-up will examine the extensions and interpretations of this exploration. For example, as we discussed in class --

Will Barney always return to his starting point? If so, will Barney always travel the same distance? Does the path create a pattern of similar triangles? Where might his starting point be so that the path would create congruent triangles? What if Barney started at a point inside the triangle? Anything special about the path if he starts at the centroid? the othocenter?

Extend the sides of the triangle and let Barney begin his journey from a point outside the triangle. His path is slightly redefined -- rather than "bouncing" when he comes to a wall, he crosses the wall to change direction and continues to travel a path parallel to a side of the triangle. Construct a GSP image and explore.

The problem is rather open-ended. Don't give up on it too early.

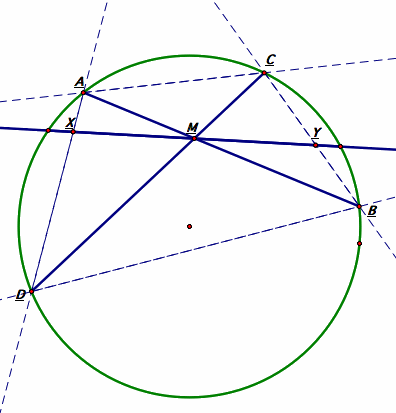
Through the midpoint M of any chord PQ of a circle, any chords AB and CD are drawn; lines AD and BC meet PQ at points X and Y. You many want to construct a line PQ containing the chord PQ. Prove that M is the midpoint of XY. Constructing a valid picture of this situation is a part of the problem, but only the first step in building the proof. Be sure that your constructions illustrate the possibilities where X and Y can be either inside the circle or outside of it.

With line PQ, construct lines AC and BD. If AC and BD are the intersections points X' and Y' with line PQ, what can you prove about the relationship of M, X', and Y'

Part Three

Course Evaluation

Return to EMAT 6680 Home Page.