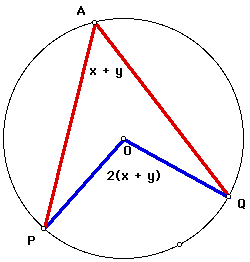
Here, I am given a circle with center O. Angle PAQ is an inscribed angle of the circle, and angle POQ is a central angle of the circle. Both angles intercept the common arc PQ. I want to prove that the measure of angle PAQ = 1/2 of the measure of angle POQ.
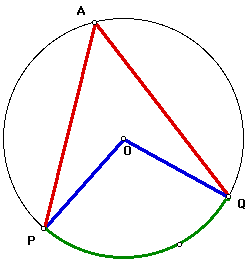
First, I construct segment OA. Obviously, segments OA, OP, and OQ are radii of the same circle. Therefore, OA = OP = OQ.
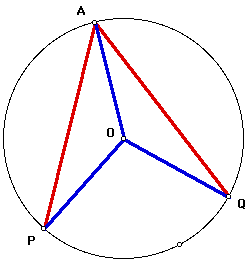
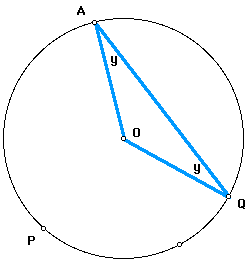
I am left with two isosceles triangles. The first is triangle POA. Since the angles opposite the congruent sides of an isosceles triangle are congruent, I know that angles OPA and OAP are congruent. I'll let their measure = x.
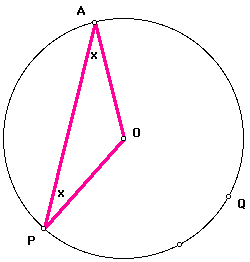
The second isosceles triangle is triangle QOA. Again, since the angles opposite the congruent sides of an isosceles triangle are congruent, I know that angles OQA and OAQ are congruent. I'll let their measure = y.
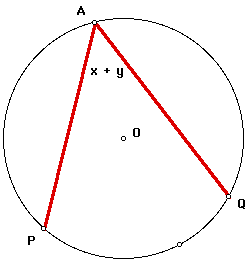
By angle addition, the measure of angle PAQ = the measure of angle OAP + the measure of angle OAQ. By substitution, the measure of angle PAQ = x + y.
Since I know that the sum of the interior angles of a triangle equals 180 degrees, then the measure of angle POA = 180 - 2x. Similarly, the measure of angle QOA = 180 - 2y.
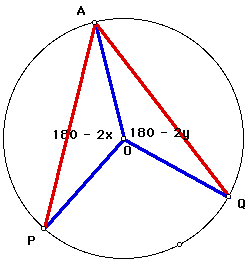
Since a circle measure 360 degrees, then the sum of its central angles must add to equal 360 degrees. Thus, the measure of angle POQ = 360 - (the measure of angle POA + the measure of angle QOA). By substitution and some simplification, the measure of angle POQ = 360 - [(180 - 2x) + (180 - 2y)] = 360 - (360 - 2x - 2y) = 360 - 360 + 2x + 2y = 2x + 2y.
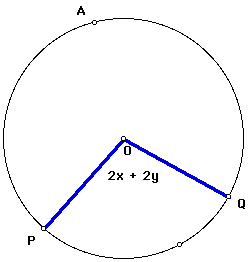
In summary, the measurement of angle PAQ = x + y, and the measurement of angle POQ = 2x + 2y = 2(x + y). Thus, the measure of angle PAQ = 1/2 of the measure of angle POQ, which was to be proved.