Polar Equations and Their Graphs
By
Janet Shiver
EMAT 6680
Investigation: We
are going to graph several different polar curves and examine their behaviors.
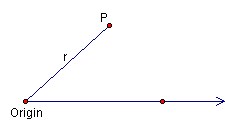
Background: A coordinate system is used to identify the location of a
point in space. Often times in mathematics we use the rectangular or Cartesian
coordinate system. This system uses a rectangular grid to describe the location
of a point. Another method for describing the location of a point is with
distance and direction from a fixed reference point. To do this we will
use the polar coordinate system. To set up the system, we must first choose
a fixed point called the origin and draw a ray from this point. This will
be the polar axis. Next we will choose any point p in the plane and rotate
a segment from the polar axis to this point. The angle formed will be θ and
the distance from the origin to the point will be r. Thus the point (r, θ)
specifies the location of the point.
Common Polar Curves
We will begin our look
at polar curves with some basic graphs.
The Archimedean Spiral

The Archimedean spiral is formed from the equation r = aθ. The graph above was created with a = ½.

r = .1θ and r = θ
By changing the values of a we can see that the spiral becomes tighter for smaller values and wider for larger values.
Circles
The graphs of the equations r = a sin θ and r = a cos θ will be circles.

r = a sin θ and r = a cos θ
Roses
Equations of the form
r = a sin nθ and r = a cos nθ produce roses.
How does the graph of r = a sin nθ vary from the graph of r = a cos n θ?

r = cos 2θ r = sin 2θ
Both the sine and cosine graphs have the same appearance. You will notice, however, that the sine graph has been rotated 45 degrees from the cosine graph. This is the same result as found in the rectangular coordinate system where the sine function has been shifted 45 degrees from the cosine function.

Now lets see what happens when we hold a constant but vary the value of n.

r = 2cos 2θ

r = 2 sin 3θ

r = 2 sin 4θ
After graphing several equations of this form we notice that when n is an odd number the rose will have n petals and when n is an even number the rose will have 2n petals. Why does this occur? When n is an odd number, the points in each petal are actually traced twice from 0 to 2pi, however, when n is even the petals are only traced once.
Next lets examine what happens as n is held constant and the value of a
varies.

r = sin 4θ r = 2 sin 4θ r = 3 sin 4θ
It appears that the value
of a is the length of each petal of the rose.
Cardioids and Limacons
Equations of the form r = a + b sin θ, a – b sin θ, a + b cos θ, and a – b cos θ will produce limacons.
Lets examine what happens for various values of a and b.

r = 2 + 3sin θ
When the value of a is less than the value of b, the graph is a limacon with and inner loop.

r = 5 + cos 4θ
When the value of a is greater than the value of b, the graph is a dimpled limacon.

r = 5 –2 sin θ
When the value of a is greater than or equal to the value of 2b, the graph is a convex limacon.

r = 2 – 2 sin θ
When the value of a equals the value of b, the graph is a special case of the limacon. It is called a cardioid.
Notice that, in each of the graphs of the liamsons, changing from sine to cosine does not affect the shape of the graph just its orientation. Equations using sine will be symmetric to the vertical axis while equations using cosine are symmetric to the horizontal axis. The sign of b will also affect their orientation.
Lemniscates
The graphs of equations of the form ![]() and
and ![]() will be lemniscates.
will be lemniscates.

![]()
This is a graph of
the lemniscate of Bernoulli.
Another Interesting Graph
This next graph is
rather intriguing. After working with several polar graphs and observing their
general shape, periodicity, and symmetry, it was quite surprising to end
up with the graph of a straight line. The graph below appears to be the
graph of the equation y = x+1.


To prove that this is actually the correct graph for this equation we will go back to the relationship between polar and Cartesian coordinates. We will use the fact that x = r cosθ and y = r sinθ to show that the polar equation is actually equivalent to the equation y = x + 1.

Since,

Thus y = x +1.
Just for Fun!
As I was researching
polar curves, I stumbled across many other interesting graphs. I have included
some of my favorites below. Enjoy!
The Conchoid of Nicomedes

![]()
Untitled

Hyperbolic Spiral


Untitled


Oscar’s Butterfly
![]()
Return to Janet Shiver’s
Home Page