I believe that this geometric proportion served the Creator as an idea

when He introduced the continuous generation of similar ojects from

similar objects.

J. Kepler (1571-1630)

We start with a problem in aesthetics. Consider a line segment. What is the most "pleasing" division of this line segment into two parts? Some people might say at the halfway point. Others might say at the one-quarters point. The "correct answer" is, however, none of these, and is found in Western art from the Ancient Greeks ownward (art theorists speak of it as the principle of "dynamic symmetry"):

A geometric definition can be given in terms of the above figure. Let the ratio x = BC/AB. The Numerator and Denominator can then be taken as AB = a and BC = x without loss of generality. Now define the position of B by

Plugging in gives

or

which can be solved using the Quadratic Equation to obtain

=

This quantity known as the Golden Ratio, Divine Proportion, etc.

The quantity

where is the Golden Ratio. The golden ratio conjugate is sometimes also called the Silver Ratio.

Click on the icon for a GSP scritp to divide a segment in golden ratio.

---

We claim that the Golden mean is intricately related to Fibonacci's sequence:

This sequence models (in a naive way) the growth of a rabbit population. Rabbits are assumed to start having bunnies once a month after they are two months old; they always give birth to twins (one male bunny, one female bunny), they never die and never stop propagating. The number of rabbit pairs after n months turns out to be

What can possibly have in common with {}? This is one of the most remarkable ideas in all of mathematics. Observe first that

.

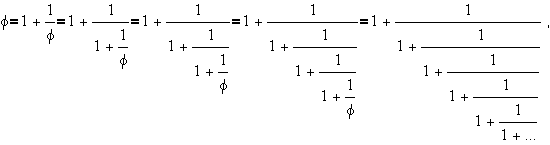an infinite continued fraction. Now look at the partial continued fractions leading up to the infinite continued fraction representation of

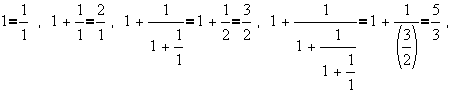
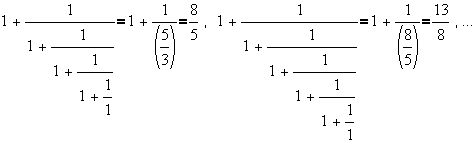
All of the resulting fractions are ratios of successive Fibonacci numbers! This motivates the theorem that:

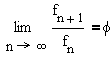
In words, as n approaches infinity, the limit of the sequence of successive Fibonacci number ratios is the Golden mean. This theorem is also true for arbitrary sequences satisfying the same recursion

as long as it is assumed that the initial terms and are distinct ([9,10,11]). For example Lucas Sequences can be considered in this sense.

For a further investigation of the relation among the Golden Ratio, Fibonacci Sequences and Lucas Sequences, Click Here.

References:

1. http://www.treasure-troves.com/math/GoldenRatio.html

2. http://www.mathsoft.com/asolve/constant/gold/gold.html

3. Huntley, H.E. The Divine Proportion: A Study in Mathematical Beauty. 1970, DoverPub., New York

4. H S M Coxeter's Introduction to Geometry, published by Wiley, in its Wiley Classics Library series, 1989