Students are introduced to the works of Pythagoreas during Pre-Algebra. The Pythagorean Theorem helps build a bridge from the variable world of basic algebra to the visual world of geometry. This essay answers the question of why the Pythagorean Theorem works along with some extras to incorporate into the lessons.

The Pythagorean Theorem states

in any right triangle the measure of the sides is given by when c is the hypotenuse.

Now notice the side measurements.

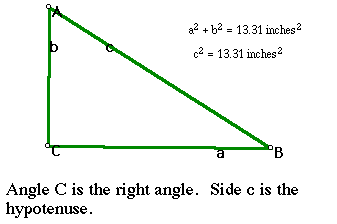
Now let's look at the right triangle on the a coordinate grid. The Distance Formula helps show why the Pythagorean Theorem works. Angle C is the right angle and is placed on the origin (0,0). The triangle is placed in a first quadrant.

.

In order to find side c, the Distance Formula is used to find the distance between points A and B. This gives the length of side c.

Let (x1, y1) = (a,0) --This is Point B

(x2, y2) = (0,b) -- This is Point A

Now plug these points into the Distance Formula.

d represents the length of side c. Therefore which is the Pythagorean Theorem.

This shows the case when Angle C is placed at the origin. Now look at the case when Angle C is not at the origin.

Now plug these points into the Distance Formula.

Let (x1,y1) = (x, b+y) -- Point A

(x2,y2) = (a+x,y) -- Point B

d represents the length of side c. Therefore which is the Pythagorean Theorem. This theorem is used to find the missing sides of right triangles.

Now notice the the Pythagorean Theorem using squares.

This helps to visualize how the squares fit into the Pythagorean Theorem. Recall the area of a square is given by s^2 when s is the side of a square.

The Converse of the Pythagorean Theorem states that if , then the triangle is a right triangle. What type of triangle is formed if the Pythagorean Theorem does not work?

Notice that <and that angle C is an obtuse angle. Therefore, if angle C is obtuse thus forming an obtuse triangle then <.

Now notice that angle C is an acute angle and >. Therefore if the triangle is an acute triangle, then >.

In summary * if , then the triangle is a right triangle

*if >, then the triangle is an acute triangle.

*if >, then the triangle is an obtuse triangle.

Return to Ruth Naugle's home page.