

![]() Check Problems from last lesson
Check Problems from last lesson
Review: Write in your Journal all that you remember from the beginning of the lesson. Don't go back yet to check. Do from memory.
![]() Check
your memory, noting what you need more work on.
Check
your memory, noting what you need more work on.
Activity: The Isosceles (45-45) Right Triangle. An Isosceles right triangle is a special triangle with several special properties. Thes properties result in shortcuts that make it easy to find unknown measures of parts of an isosceles right triangles
Click here and print the GSP activity.
Activity: The 30-60-90 Right Triangle. The right triangle, which is half of an equilateral (equiangular) triangle, has special properties also.
Click here and print the GSP activity
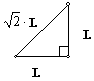 Isosceles
Right (
Isosceles
Right (![]() )Triangle Theorem: In
an isosceles right (
)Triangle Theorem: In
an isosceles right (![]() ) triangle, the
hypotenuse is
) triangle, the
hypotenuse is ![]() times as long as
a leg.
times as long as
a leg.
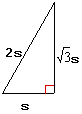
![]() Triangle Theorem:
In a
Triangle Theorem:
In a ![]() triangle,
the hypotenuse is twice as long as the shorter leg and the longer
leg is
triangle,
the hypotenuse is twice as long as the shorter leg and the longer
leg is ![]() times as long as the shorter leg.
times as long as the shorter leg.
 In the triangle to the right we
can apply the Pythagorean thereom to the hypotenuse, s :
In the triangle to the right we
can apply the Pythagorean thereom to the hypotenuse, s :
So we see that the sides in a ![]() triangle
are
triangle
are ![]() .
.
Examples of using the Isosceles Right
Triangle and ![]() Theorem:
Theorem:
Find x:
1. Since we have an isosceles right
(
Since we have an isosceles right
(![]() ) triangle, the legs are equal, so
x =12.
) triangle, the legs are equal, so
x =12.
2.  Since we have an isosceles right
(
Since we have an isosceles right
(![]() )
triangle, the hypotenuse is
)
triangle, the hypotenuse is ![]() as long
as the leg so
as long
as the leg so
x = 12![]() .
.
Find the Area of the following triangle:
We are given the length of the hypotenuse so we will first
use this part of the ![]() Theorem
which states: the hypotenuse is twice the shorter leg, so the
shorter leg (the base of our triangle) is half the
hypotenuse,or,
Theorem
which states: the hypotenuse is twice the shorter leg, so the
shorter leg (the base of our triangle) is half the
hypotenuse,or, ![]() feet.
feet.
The next part of the theorem says longer leg is ![]() times
as long as the shorter leg. So the altitude of our triangle (the
longer leg) is
times
as long as the shorter leg. So the altitude of our triangle (the
longer leg) is ![]() feet. The formula
for the area of a triangle is
feet. The formula
for the area of a triangle is ![]() base
times altitude, so we can find the area of our triangle is :
base
times altitude, so we can find the area of our triangle is :![]() feet.
feet.