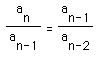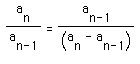University of Georgia
*see other examples
Fibonacci and the Golden Ratio
The relationship between the Fibonacci Sequence and
the Golden Ratio is a surprising one. We have two seemingly unrelated
topics producing the same exact number. Considering that this
number (or Golden Ratio) is non-rational, the occurance is beyond
coincidence. It calls for futher examination...
The Golden Ratio = (sqrt(5) + 1)/2 or about 1.618
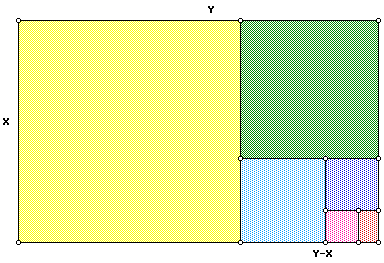
The Golden Ratio is, perhaps, best visually displayed
in the Golden Rectangle. This rectangle has the property that
its length is in Golen Ratio with its width. As a consequence,
we can divide this rectangle into a square and a smaller rectangle
that is similar to the first. Let the following GSP sketch illustrate:
The Fibonacci Sequence is one where each term is defined
as the sum of the two previous terms:
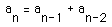 We can create this sequence easily in a spreadsheet,
using the formula above. This has been done in the center column
of the spreadsheet below:
We can create this sequence easily in a spreadsheet,
using the formula above. This has been done in the center column
of the spreadsheet below:
| 1 |
1 |
|
| 2 |
1 |
1 |
| 3 |
2 |
2 |
| 4 |
3 |
1.5 |
| 5 |
5 |
1.66666666666667 |
| 6 |
8 |
1.6 |
| 7 |
13 |
1.625 |
| 8 |
21 |
1.61538461538462 |
| 9 |
34 |
1.61904761904762 |
| 10 |
55 |
1.61764705882353 |
| 11 |
89 |
1.61818181818182 |
| 12 |
144 |
1.61797752808989 |
| 13 |
233 |
1.61805555555556 |
| 14 |
377 |
1.61802575107296 |
| 15 |
610 |
1.61803713527851 |
| 16 |
987 |
1.61803278688525 |
| 17 |
1597 |
1.61803444782168 |
| 18 |
2584 |
1.61803381340013 |
| 19 |
4181 |
1.61803405572755 |
| 20 |
6765 |
1.61803396316671 |
| 21 |
10946 |
1.6180339985218 |
| 22 |
17711 |
1.61803398501736 |
| 23 |
28657 |
1.6180339901756 |
| 24 |
46368 |
1.61803398820533 |
| 25 |
75025 |
1.6180339889579 |
| 26 |
121393 |
1.61803398867044 |
| 27 |
196418 |
1.61803398878024 |
| 28 |
317811 |
1.6180339887383 |
| 29 |
514229 |
1.61803398875432 |
| 30 |
832040 |
1.6180339887482 |
| 31 |
1346269 |
1.61803398875054 |
| 32 |
2178309 |
1.61803398874965 |
| 33 |
3524578 |
1.61803398874999 |
| 34 |
5702887 |
1.61803398874986 |
| 35 |
9227465 |
1.61803398874991 |
| 36 |
14930352 |
1.61803398874989 |
| 37 |
24157817 |
1.6180339887499 |
| 38 |
39088169 |
1.61803398874989 |
| 39 |
63245986 |
1.6180339887499 |
| 40 |
102334155 |
1.61803398874989 |
| 41 |
165580141 |
1.6180339887499 |
| 42 |
267914296 |
1.6180339887499 |
| 43 |
433494437 |
1.6180339887499 |
| 44 |
701408733 |
1.6180339887499 |
| 45 |
1134903170 |
1.6180339887499 |
| 46 |
1836311903 |
1.6180339887499 |
| 47 |
2971215073 |
1.6180339887499 |
| 48 |
4807526976 |
1.6180339887499 |
| 49 |
7778742049 |
1.6180339887499 |
| 50 |
12586269025 |
1.6180339887499 |
We have also taken the ratio of every two consecutive
terms, in the right column. If we take the limit of this ratio
as the terms get larger... the Golden Ratio!
Understanding the Relationship
Remember, now, that the Golden Rectangle can be divided
into a square and another Golden Rectangle. In fact, we can repeat
this process time and again. Suppose we start with a rectangle
with length Y and width X. When we divide this rectangle into
a square and a new Golden Rectangle, we get length X and width
Y-X for the new rectangle. Since the sides of the rectangles are
in the same proportion (namely 1.618...), we get:
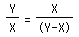 Now, let's return to the Fibonacci Sequence. The ratio
of consecutive terms forms a sequence itself. Suppose we know
that this sequence converges to some real number (we can prove
this in a lesson on geometric sequences). Then, for large values
of n:
Now, let's return to the Fibonacci Sequence. The ratio
of consecutive terms forms a sequence itself. Suppose we know
that this sequence converges to some real number (we can prove
this in a lesson on geometric sequences). Then, for large values
of n:
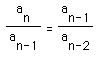 But
But 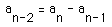 , so
, so
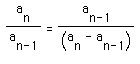 And, if we replace
And, if we replace 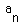 with Y and
with Y and 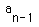 with X, we have
with X, we have
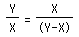 The Golen Ratio!
The Golen Ratio!