
Conic Sections

Introduction
Conic sections were discovered by Menaechums, a Greek mathematician,
in the third or fourth century BC. He dicovered conics while he was trying
to solve the problem of doubling a cube. He was the first to show that the
conics could be obtained by cutting a cone with a plane. Much of our knowledge
about the early history of conics is due to the works of Apollonius. Apollonius,
another Greek mathematician, wrote an eight book collection titled Conic
Sections in the second century BC. Apollonius supplied the names ellipse,
parabola, and hyperbola to describe the shapes of the conics. The early
Greeks were primarily concerned with the geometrical properties of conics.
It wasn't until the 16th and 17th centuries that people began to use conics
to solve pratical problems. Mathematicians and astronomers such as Copernicus,
Galileo, Johann Kepler, and Issac Newton used conics to describe the motions
of objects on the earth and in space.
The third way is to define the conics as a locus of points satisfying
a certain geometric property. This is the approach that we are going to
take.
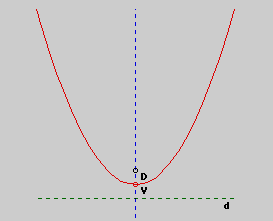
In the above diagram, V is the vertex of the parabola, D is the focus,
and d is the directrix.
if the parabola is along the vertical axis and
if the parabola is along the horizontal axis.
Here we would like the students to investigate parabolas using Algebra
Expresser and GSP. In Algebra Expresser the students would look at the standard
equation of a parabola. The students would then investigate this equation
by varying values for h,k, and a. What happens to the parabola as each value
is increased or decreased? What happens if a is negative?
For GSP construction the students would begin by constructing an arbitrary
line and an arbitrary point. Now, create a point on the line by choosing
the Point on Object command from the Constuct menu. Your challenge is to
construct the line that represented the crease in your paper . You might
want to look back at your paper folding exercise to get a clue as to how
you would do this. After you construct this line, select it and choose the
Trace Locus command from the Display menu. As you drag point D back and
forth along line j you'll trace the outline of your curve.
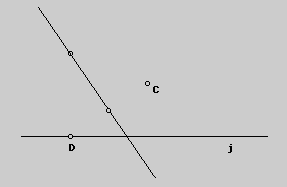
Experiment with different locations of point D to see the change in appearance
of the curve you trace. Describe your findings. Also describe what happens
to the curve when you drag and rotate line j.

The vertices are located at the intersection of the line through the foci and the ellipse. The segment joining the two vertices is called the major axis and its midpoint is the center of the ellipse labeled C is the above sketch. The chord perpendicular to the major axis and passing through the center is called the minor axis.
Hands on investigations of the ellipse
Ellipse - paper folding
Materials needed
wax paper
compass
Instructions
1. Draw a circle on the wax paper
2. Label the center of the circle C
3. Pick a point F inside the circle
4. Select a point A on the circle and fold the paper so that point
A coincides with point F
5. Make a sharp crease in the paper to keep track of this fold
6. Continue this process by picking other points on the circle until you
can identify the type of curve being produced.
7. Discuss the results with your classmates. What are the similarities and
differences between the shapes you and your classmates have made?
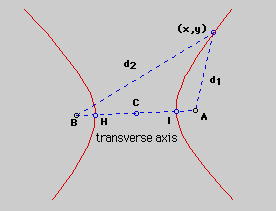
In the above figure, A and B are the foci, C is the center of the hyperbola, H and I are the vertices and d(1) and d(2) are the distances to the foci from (x,y).
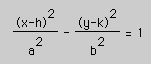
if the transverse axis is horizontal and
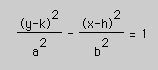
if the transverse axis is vertical.
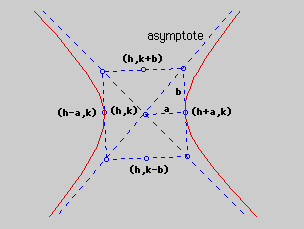
If the transverse axis is horizontal, the equation for the asymptotes
are
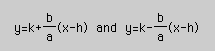
and if the transverse axis is vertical, the equation for the asymptotes
are
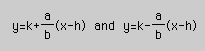
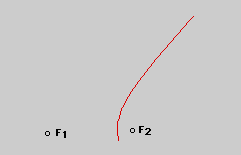
Materials needed
ruler
Steps
1. Choose a point A on the incomplete hyperbola shown above. Measure
the distance AF1 and AF2.
2. There is exactly one more point B on the hyperbola such that AF1=BF1
and AF2=BF2. Draw and label this point in the figure above.
3. There is at least one more point C on the hyperbola such that
AF1=CF2 and AF2=CF1. Find all points meeting these conditions and draw and
label them.
4. Use the above information and draw the rest of the hyperbola.
5. Compare with your classmates.

Once you are finish answer the following questions.
1. What happens when you move point F closer to the edge, closer
to the center, on the circle, and outside the circle?