This essay was inspired by a class that I am taking this quarter. The
class is the History of Mathematics. In this class, we are learning
how to include the history of mathematics in teaching a mathematics. One
way to include the history of mathematics in your classroom is to incorporate
ancient mathematics problems in your instruction. Another way is to introduce
a new topic with some history of the topic. Hopefully, this essay will give
you some ideas of how to include the history of the Pythagorean Theorem
in the teaching and learning of it.
We have been discussing different topics that were developed in ancient
civilizations. The Pythagorean Theorem is one of these topics. This theorem
is one of the earliest know theorems to ancient civilizations. It was named
after Pythagoras, a Greek mathematician and philosopher. The theorem bears
his name although we have evidence that the Babylonians knew this relationship
some 1000 years earlier. Plimpton 322, a Babylonian mathematical
tablet dated back to 1900 B.C., contains a table of Pythagorean triples.
The Chou-pei, an ancient Chinese text, also gives us evidence that
the Chinese knew about the Pythagorean theorem many years before Pythagoras
or one of his colleagues in the Pythagorean society discovered and proved
it. This is the reason why the theorem is named after Pythagoras.
Pythagoras lived in the sixth or fifth century B.C. He founded the Pythagorean
School in Crotona. This school was an academy for the study of mathematics,
philosophy, and natural science. The Pythagorean School was more than a
school; it was "a closely knit brotherhood with secret rites and observances"
(Eves 75). Because of this, the school was destroyed by democratic forces
of Italy. Although the brotherhood was scattered, it continued to exist
for two more centuries. Pythagoras and his colleagues are credited with many
contributions to mathematics.
The following is an investigation of how the Pythagorean theorem has been
proved over the years.
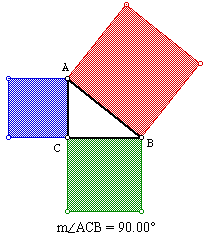
Pythagorean Theorem
The theorem states that:
"The square on the hypotenuse of a right triangle is equal to the sum of the squares on the two legs" (Eves 80-81).
This theorem is talking about the area of the squares that are built on
each side of the right triangle.

Accordingly, we obtain the following areas for the squares, where the green and blue squares are on the legs of the right triangle and the red square is on the hypotenuse.
area of the green square is
area of the blue square is
area of the red square is
From our theorem, we have the following relationship:
area of green square + area of blue square = area of red square or
As I stated earlier, this theorem was named after Pythagoras because he
was the first to prove it. He probably used a dissection type of proof similar
to the following in proving this theorem.
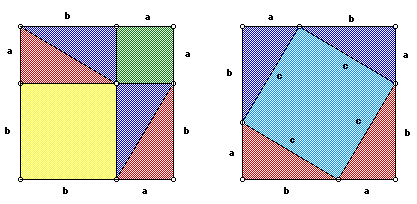
The area of the first square is given by (a+b)^2 or 4(1/2ab)+ a^2 + b^2.
The area of the second square is given by (a+b)^2 or 4(1/2ab) + c^2.
Since the squares have equal areas we can set them equal to another and
subtract equals. The case (a+b)^2=(a+b)^2 is not interesting. Let's do the
other case.
4(1/2ab) + a^2 + b^2 = 4(1/2ab)+ c^2
Subtracting equals from both sides we have
concluding Pythagoras' proof.
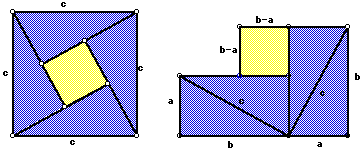
In the above diagrams, the blue triangles are all congruent and the yellow
squares are congruent. First we need to find the area of the big square
two different ways. First let's find the area using the area formula for
a square.
Thus, A=c^2.
Now, lets find the area by finding the area of each of the components and
then sum the areas.
Area of the blue triangles = 4(1/2)ab
Area of the yellow square = (b-a)^2
Area of the big square = 4(1/2)ab + (b-a)^2
= 2ab + b^2 - 2ab + a^2
= b^2 + a^2
Since, the square has the same area no matter how you find it
A = c^2 = a^2 + b^2,
concluding the proof.

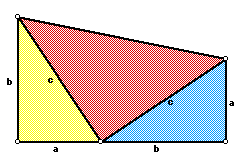
Now prove that triangles ABC and CBE are similar.
It follows from the AA postulate that triangle ABC is similar to triangle
CBE, since angle B is congruent to angle B and angle C is congruent to angle
E. Thus, since internal ratios are equal s/a=a/c.
Multiplying both sides by ac we get
sc=a^2.
Now show that triangles ABC and ACE are similar.
As before, it follows from the AA postulate that these two triangles are
similar. Angle A is congruent to angle A and angle C is congruent to angle
E. Thus, r/b=b/c. Multiplying both sides by bc we get
rc=b^2.
Now when we add the two results we get
sc + rc = a^2 + b^2.
c(s+r) = a^2 + b^2
c^2 = a^2 + b^2,
concluding the proof of the Pythagorean Theorem.
First, we need to find the area of the trapezoid by using the area formula
of the trapezoid.
A=(1/2)h(b1+b2) area of a trapezoid
In the above diagram, h=a+b, b1=a, and b2=b.
A=(1/2)(a+b)(a+b)
=(1/2)(a^2+2ab+b^2).
Now, let's find the area of the trapezoid by summing the area of the three
right triangles.
The area of the yellow triangle is
A=1/2(ba).
The area of the red triangle is
A=1/2(c^2).
The area of the blue triangle is
A= 1/2(ab).
The sum of the area of the triangles is
1/2(ba) + 1/2(c^2) + 1/2(ab) = 1/2(ba + c^2 + ab) = 1/2(2ab + c^2).
Since, this area is equal to the area of the trapezoid we have the following
relation:
(1/2)(a^2 + 2ab + b^2) = (1/2)(2ab + c^2).
Multiplying both sides by 2 and subtracting 2ab from both sides we get
concluding the proof.