Suppose there is some rectangular-shaped builder in the scenario given above and your first attempt is to draw a rectangle on the canvas. You realize that your drawing seems distorted even though you drew the shape that you saw. This was the problem that was addressed by artists like Leonardo de Vinci in the fifteenth century. At that time in history the artists developed a theory of perspective in order to realistically paint two-dimensional representations of three-dimensional scenes. By the nineteenth century mathematicians began studding the properties involved in transferring a three-dimensional object to a two-dimensional canvas. Projective geometry involves the study of these properties.
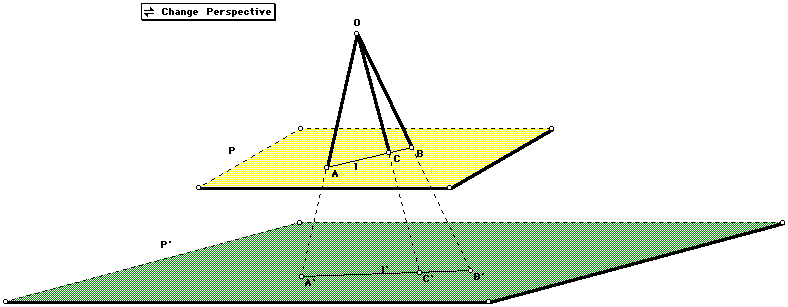
To begin this investigation, consider the following illustration: Let the point O correspoind to the eye of the viewer, the green plane, P', corresponds to what the artist actually sees; the yellow plane, P, corresponds to the canvas. Therefore, from the point O, the lines l and l' are the same.

Exercise one involves one of the earliest discoveries pertaining to projective geometry:
Topic One.
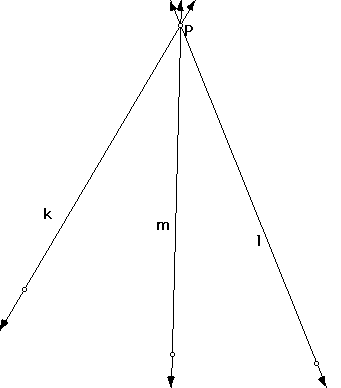
1. Construct three lines l, m, & k intersecting in a point P. You should have something like the following:
2. Select 3 points A, B, and C such that A lies on k, B lies on m, and C lies on l. Then select 3 other points A', B', and C' such that A' lies on k, B' lies on m and C' lies on l.
3. Construct triangles ABC and A'B'C'.

4. Construct lines AC and A'C' and mark the point of intersection, X.
5. Construct lines AB and A'B'; mark their point of intersection, Y.
6. Construct lines BC and B'C'; mark their point of intersection, Z.

If you don't want to do this construction, here is GSP file:(Click here.)
7. Is there anything of interest about the points of intersection, X, Y,
Z?
8. Investigate what happens to the line when the triangles are
placed in different positions?
9. In particular, consider what happens when 2 corresponding side are parallel?
10. In general, what can be concluded from this exercise?
"If the vertices of two triangles correspond in such a way that the lines joining corresponding vertices are concurrent, then the intersections of corresponding sides are collinear."
The following are exercises pertaining to the above result. These can be assigned as homework/classwork.
1. Suppose you are given a piece of paper on which someone has drawn a point A and two lines l' and l'', neither passing through A and whose point of intersection lies off the paper. You are asked to draw the line through A which goes through that point of intersection. How do you do it?
(Hint: Pick a on l', b on l'', and let A=c. Let a' be on l' and b' on l'' be chosen so that lin ab is parallel to a'b', and choose c' so that line ac is parallel to line a'c' and line bc is parallel to line b'c'.)
2. You are given a short straightedge and two points P & Q a great distance apart. Use your short straightedge to draw the line joining P and Q. (Hint: Use 1 above)
Topic two.
1. Construct 2 non-parallel .lines l and m
2. Pick 3 points, P, Q, and R on l and 3 points P', Q', and R' on m.

3. Construct lines PQ', PR', QP', QR', RQ', and RP'.
4. Consider PQ' and QP'; PR' and RP'; and RQ' and QR'. Your figure
should look similar to the following:

5. What is interesting about these points of intersection?
(They are collinear.)
6. Move all points around even to the extent of changing their
relative positions. Make a general statement you believe to be
true about the relationship(s) you have noted.
The general statement that can be conjectured from the above result is known as Pappus's Theorem; i.e., Let P, Q, R and P', Q', R' be collinear triples of points. Denote the intersection of line
PQ' and P'Q by X; the intersection of line PR' and RP' by Y; the intersection of line QR' and line Q"R by Z. Then the points X, Y, & Z lie on a line also, i.e., X, Y, Z are collinear points.
The following can be used as homework/classwork.
1. If the point A is the intersection of lines PQ and P'Q' ; point B the intersection of lines QR and Q'R'; and point C the intersection of lines PR and P'R', then A, B, & C lie on the same line.
Topic 3.
Extension of topic 2: (Pascal's Theorem)
Let A, B, C, A', B', C' be six distinct points on a nondegenerate conic. Then the three points of intersection, X, Y, & Z , where X is the intersection of lines AB' and BA', Y is the intersection of lines
AC' and CA', and Z is the intersection of lines BC' and CB', lie on the same line.
Topic 4.
Cross Ratio.
Consider the following situation: If you have 3 points, A, B, and C on a line, when you project to another line as in the picture below, the ratio of the lengths AB and BC is not the same as the corresponding ratio of A'B' and B'C'.
Now observe what happens when we add a fourth point, D. (Click here.)
<