

INTRODUCTION
Objectives: 1. Students will recognize maximum and minimum values of a function from a
graph and from a table of values.
2. Students will determine the maximum and minimum values of a function
representing a real life situation.
ACTIVITY 1
Using a prepared transparency, the teacher will lead students in a discussion of what the
minimum and maximum values of a function are. Have students look at several graphs and determine the relative maximum and minimum values. Click below for sample graphs.
GRAPH 1
GRAPH 2
GRAPH 3
GRAPH 4
ACTIVITY 2
Given a discrete set of data, determine the maximum and minimum values of the function.
The spreadsheet is an excellent way to generate values of a function. Click here for a sample spreadsheet. SPREADSHEET
Assignment: Instruct students to sketch graphs given certain maximum and minimum
values.
INVESTIGATION 1
Activity 1
Today's lesson revolves around a classic optimization problem of maximizing the
volume of a box.
a. Divide class into groups of 3 or 4. Give each group a sheet of paper. Illustrate the
act of creating a box by cutting equal squares from each corner and turning up.
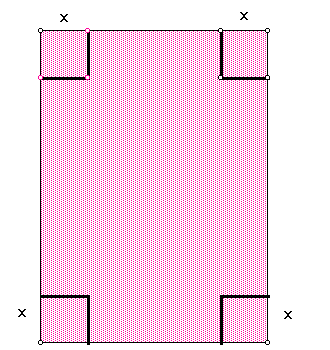
b. Give each. group a different side measure of X for the square to be cut off.
Use x = 1 ,2,3,4,5,6,7 and 8. Discuss what happens if the side measure
is equal to 9. This would be an appropriate time to discuss the domain
of the x value.
c. Ask the class which basic shape would seem to yield a maximum value. Should
the box be tall, short, or cubical? Discuss each groups volume and which appears
to have maximum volume. Ask "What about other values of "x" besides integers?
Could x = 3.5? How can we look at all possible values of s and its corresponding
volume?".
d. Have each group make its box and determine its volume. Then, each group should
discover a general formula for the volume of a given any value of x. Compare
each groups volume to the shape of their box and then compare each groups general
volume formula to the other groups. Decide on the formula which best defines
the volume for a box.
Activity 2
a. The equation determined for the volume of a box created by cutting out a square of
area "x2" should be V=(x)(18 - 2x)(24 - 2x). Using this equation, we will now
explore two methods of looking at all values of x that will produce a reasonable
volume and how to locate these values through use of the spreadsheet and use of a
graphing tool.
b. If you click on Microsoft Excel, you will see a demonstration of how Microsoft
Excel is used to locate the length of the side of the square which gives the
maximum volume.
Directions
1. Students should begin by typing 1 into the A1 slot. To increase each time by
an increment of 0.1, type `a1 + .1' into the A2 slot. Click on a2 and fill
down to about row 100. Now go back up to B1 and type your volume
formula discovered earlier using `a1' for `x'. Click on B1 and fill down
to discover all the volumes. Find where the volume is the largest and its
corresponding x value will tell you the dimensions of the square to remove
from each corner to create maximum volume.
2. How close were their original guesses to what they thought would be the
dimensions of the box?
3. Have them create a box with this new dimension to discover what its shape
will be. How does it compare with the earlier discussion?
c. If you click on Algebra Expressor, you will see a demonstration of how Algebra
Expresssor is used to locate the length of the side of the square which gives the
maximum volume.
Directions
1. Graph the equation you discovered for the volume of the box. You will
have to adjust the domain as determined earlier and also the range values
until you have a complete graph in view. Use the trace function to discover
the x-value which gives the maximum y-value on that curve. This x-value
should be close to the value discovered by Excel if not identical.
2. How would you determine the dimensions of a box that has a specific
volume?
d. ASSIGNMENT: Students should write-up this assignment including the steps
taken to complete each activity, its resulting outcome, and any discoveries
made.
INVESTIGATION 2
Investigate: Why do bees use a hexagonal shape rather than some other shape to build their honeycombs?
Help students to see the two main issues:
1) What other shapes would fill the plane?
2) Given a fixed perimeter for the cross-section of one cell of the honeycomb,
which shape provides the maximum volume for the enclosed space?
Activity 1
Give students some pattern blocks (use only regular polygons) and ask them to see which ones will fill the plane. Have students complete the following chart for those polygons that do fill the plane.
| | Number of Tiles | Measure of
Shape of Tile | Number of sides | Around a Point | One Angle____
| | |
____________ |__________________|_________________ |_______________
| | |
____________ |__________________|_________________ |_______________
Activity 2
Give each group of students eight strips each measuring 2 cm by 24 cm cut from heavy paper and instruct them to construct a cross-section of a honeycomb. Have some groups construct a comb of hexagonal cells, others, a comb with square cells, and the rest a comb with triangular cells. In all cases the perimeter of a single cell will be 24 cm.
Have students compute the area of each. Ask: Given the depth of each cell is the same and the perimeter of each cell is the same, which shape would hold the most honey? Which shape would provide the most economical use of the wax?
Activity 3
Using x for fixed perimeter, express the cross sectional area of each of the three types of cells as a function of x. Using Algebra Expressor, graph the three functions (each is a quadratic). Discuss with your students the domain and range for the problem situation. Students could trace the graphs to find the maximum area for each shape within the appropriate domain.
Click here to view the graphs of the functions.
Activity 4
Have students use a spreadsheet to compute areas of the three shapes we have discussed increasing the length of a side by 0.1 cm each time. Students could then verify the results found previously.
Click here to view sample spreadsheet.
Assignment: Students will write a paper describing the procedures used in these activities and their conclusions.
INVESTIGATION 3
You are the captain of a ship, and one of your passengers has been injured. Your ship is 30 miles from a point that is 60 miles downshore from a hospital. You must order an ambulance to meet your ship's dinghy at any point along a road that runs parallel to the shoreline. You would like to meet the ambulance at a point that will get your passenger to the hospital in the shortest possible time. The dinghy travels at a rate of 30 mph and the ambulance will average 50 mph.. At what point along the road should you ask the ambulance to meet you in order to minimize the amount of time?
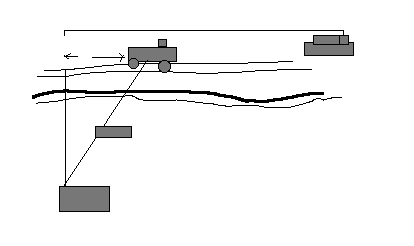
Activity 1
Be sure students understand the problem. Have them guess where they think the dinghy should meet the ambulance to minimize the time.
Then ask the following questions:
1. What is the minimum distance the dinghy would have to travel? How far would the passenger ride in the ambulance in this scenario? What would be the total travel time in this scenario?
2. Suppose in the figure above x = 10 miles.
a) How far must the dinghy travel? How long will it take the dinghy to travel this distance?
b) How far must the passenger ride in the ambulance? How long will this take?
c) How long (travel time) will it take to get the passenger to the hospital?
Activity 2
Use a spreadsheet to solve the problem. Click below to bring up EXCEL. Notice that the
headings have been entered. Lead students to suggest how to enter the formulas.
Activity 3
Click below to solve the problem using GSP. Drag on the "ambulance" and note the change in
total time. For what value of x is the total time a minimum? Is there more than one answer?
Activity 4
Use Algebra XPresser to solve the problem. Have students write the total time as a function of
x. They should then enter this function on Algebra XPresser and determine the value of x which
minimizes the function.
Assignment: Have students choose the method of solution they preferred and explain why in
a journal writing.
ASSESSMENT
Have students to work in groups to solve the following problem. Allow them to use any method or technology they find appropriate. They should solve the problem and write a paragraph describing their method.
A soft drink can has a volume of 355 cc. Determine the radius and
the height of the can that will minimize the surface area.