PATTERNS

In this activity, the term "unit side" is used to mean a side
of a unit square. For
example, in the second shape above there are 12 sides.
1. Use a geoboard and rubberbands to make the next three shapes in the pattern.
2. How many unit sides are there in the 4th, 5th, and 6th shapes?
3. How many would there be in the 10th shape?
4. If n represents the number of unit sides in a shape of the pattern, how
could you represent the
number of unit sides in the next shape?
5. If the pattern were continued, would any shape have 125 unit sides? 126
unit sides?
6. The table below shows the relationship of the number of unit squares
to the perimeter in each
shape of the pattern. Complete the table.
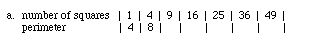
b. Let the horizontal axis represent the number of squares and the vertical
axis represent the perimeter and plot the points.
c. Describe any pattern you see in thegraph.
d. Use your graph to predice the perimeter if there are 144 squares.

