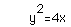
Conic sections in the form of an ellipse, a hyperbola, or a parabola are obtained by slicing a right circular cone by a plane, or, as the locus of a point which moves so its distance from a fixed point (the focus) is a constant ratio to the distance from a fixed line (the directrix).
The shape of the curve is determined by this ratio, which is called the eccentricity and is denoted by e. For the ellipse, e < 1; for the parabola, e = 1; for the hyperbola, e > 1. Since the parabola has a single value for e, it always has the same shape. However, if the eccentricities of the ellipse and hyperbola are the golden section (1.61803), interesting results are obtained. In the figure below, you will see the following graphs:
the parabola:
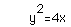
the ellipse:
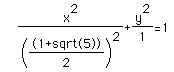
the hyperbola:
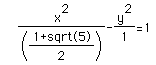
and the asymptotes (positive and negative):
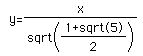
where
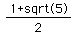
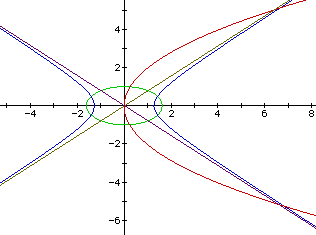
So, in the graph above where each of the equations are represented, we get the following results:
1. The latus rectum of the parabola is the directrix of the hyperbola.
2. The directrix of the parabola is the image in the y-axis of the directrix of the hyperbola.
3. The hyperbola asymptotes intersect the parabola in the points
(4P, 4[[radical]]P) and (-4P, -4[[radical]]P).
Back to Teresa Banker's Home Page