by
Mike Callinan and Larry Shook
In the following discussion, we will examine sequences and series in a variety of ways. The primary focus will be to show how GSP and Excel can be used to explore these concepts.
Mathematical concepts began early in the history of man. From earliest times, crude understanding of mathematical relationships were observed, at least quantitatively, in the physical world. The great breakthroughs in mathematics come when these concepts are generalized. In the following discussion, we will examine how specific situations involving proportions can be useful in leading to generalizations in which valid rules can be stated. We will begin with a specific instance of a constant geometric ratio and from this we will try to arrive at a general case.
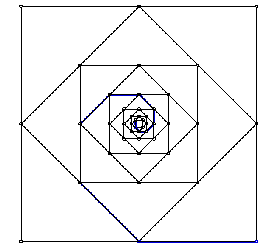
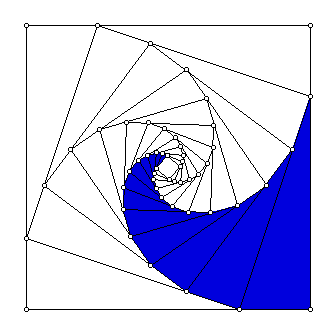
Suppose we construct the midpoints of a square of length 1 and then connect the midpoints to form another square. In repeating this process, a sequence of concentric squares are generated connected at the midpoint of the outer square. Consider the spiral formed by the sequence of segments starting at a corner and moving inward as each midpoint is reached. The spiral is highlighted in blue in the following sketch.

What is the length of the spiral as this process is continued? If we look at the first few lengths of each segment, a pattern emerges. These terms are
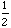 ,
,
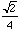 ,
,
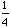 ,
,
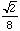 ,
,
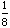 ,
,
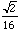 ,
,
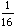 ,...
,...
From this we obtain that the lengths of each segment form a geometric series and that the length of the spiral is
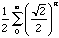 .
.At this point, we have
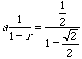 = 1 +
= 1 +
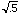 or 1.7071.
or 1.7071.
Additionally, we can look at the polygonal area formed between two of these spirals. This area is highlighted in blue in the figure below.

From the sketch, it is easy to see that the area formed by the two spirals is going to be the sum of the areas of the corner triangles in each of the concentric squares. Using the Pythagorean Theorem, we obtain the following ratio and corresponding sum
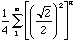 .
.For each of the above sums, we can use spreadsheets to explore the rate of convergence and find both the length and area to the desired degree of accuracy.
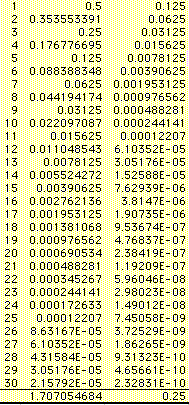
From the spreadsheet, we can observe that the sum of the lengths of the first 30 segments is approximately 1.7071 which coincides with our earlier results. Similarly, we have that the polygonal area after 30 iterations is one-fourth. As you examine the sketch of the polygonal region, this coincides with what we observe looking at the triangular regions with respect to the entire square.
Can these results be generalized for any point on the edge of the square or are they specific to the midpoint? Consider the following sketch.
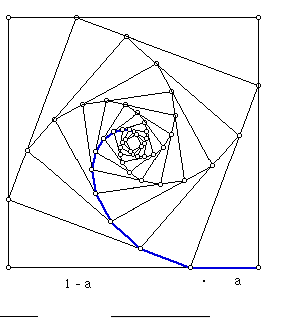
In the above sketch, the first segment of the spiral is labeled as having length "a" making the remainder of the side "1-a". Using the Pythagorean Theorem, we can generalize the lengths of the first few segments of the spiral as
a, a
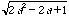 ,
a(
,
a(
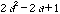 ),
a(
),
a(
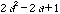 )
)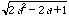 ,...
,...
The sum of the segments of the spiral can be expressed as the following geometric series
L = a
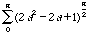 .
.
For the area enclosed by two spirals, we obtain the following sketch.
Again, we wish to establish a general rule for the area of the polygonal region which can then be used on a spreadsheet for any value of "a". We can use the Pythgorean Theorem again to establish the area of the polygonal region as
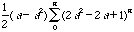 .
.Once we have the general rules established, we are able to use spreadsheets to find the length and area for different values of "a".
It is also important to take into account the rate of convergence for different values of a. For each of the following values of "a", the length is given with 3 decimal place accuracy.
n a Length Area
1200 .99 99.5019194 .25
40 .75 3.58090464 0.249999999
35 .25 1.1933932 0.249999982
30 .50 1.707054684 .25
1200 .05 1.02646013 0.249999929
1000 .01 1.00503081 0.249999999
As the general case is obtained, we are able to find the lengths and areas
between spirals with relative ease using spreadsheets. From this, we are able
to make several conjectures concerning both the length of the spirals and the
area between spirals. The length of the spirals seem to converge towards 1 as a
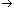 0
(the length of the side of the original square) and the polygonal area formed
by the two spirals is constant.
0
(the length of the side of the original square) and the polygonal area formed
by the two spirals is constant.
As we have explored the problem, we have been able to find a number of
relationships that exist, however, there are several extensions which could be
explored further. Does the length of the spiral converge to the length of the
side for any regular polygon as a
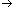 0?
Is the area between two spirals a fixed number perhaps equal to 1 over the
number of sides?
0?
Is the area between two spirals a fixed number perhaps equal to 1 over the
number of sides?
Back to Mike Callinan's Home Page