

Objectives:
- Students should be able to graph exponential functions and evaluate exponential
expressions.
- Students should be able to use exponential functions to model real life
situations such as the depreciation of a cars value.
On the board when the students enter the room are these two graphs:
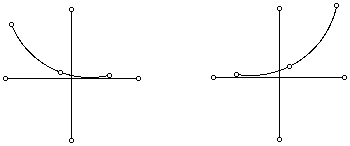
Questions to be asked:
Why do you think A can not be 1? 0?
Why do you think A can not be a negative number?
The above graph shows -A^x but the graph of (-A)^x is only points on
the graph.
Everyone put these equations into the y= screen: y1= 2^x y2=-2^x y3=(-2)^x
( you will need to use the carrot button).Now go to the table of values-
What is different about y1 and y2 ? How is y3 different from y1 or y2?
If you have y=-2^x and let x=2 then what is y? y= (-1)2*2= -4
What about y=(-2)^x and let x=2 then what is y? y=(-2)(-2)=4
***In the homework tonight when it says to sketch the graphs of f(x)= -6^x
then you will sketch the graph of y=-1*(6^x).
Transparency of the following:
Suppose that you purchased a new car for 8000 in 1991. If the value of the
car decreases by 10% each year to 90% of its previous value what is the
car worth today?
On the board
A= P(1-r)^t What is P?
A= 8000(1-r)^t What is r? r needs to be in decimal form A= 8000(1-.10)^t
What is t? (1991-1997)
A= 8000(1-.10)^6
A= 4251
?? How can we make a graph of this function? Remember what an exponential
function looks like
What about y= 8000(.90)^x graph this on your graphing calculator
What do you see? What should we set the window to be?
xmin=0 xmax=20 ymin= 0 ymax= 8000 yscl=1000
This graph will show us the value of the car at any age.
?? Use your trace key and find the value of the car if it is 15 yr. old?
=1647
What is the value to 3 decimal places? =1647.129 (go to table)
Students will be able to explore with different values and years. They should
get a good understanding how the independent and dependent varaible works.
Go over transparency #2
In 1990, you bought a television for $600. Each year, for t years, the value,
v, of the television decreases by 8%. Write an exponential model that describes
this situation.
V= 600(1-.08)^t
Objectives: Evaluate logarithmic expressions algebraically and with calculators
Convert between exponential and logarithmic form
I. Warm-up:
If a^n=a^x, then x=n. Ex. If 3^2=3^x, then x = 2.
Solve for x:
2^x=16
3^x=27
5^x=1/25
-2^x=-8
Evaluate: 3^-3, 5^-3, 10^0, 597^0, 10^-2, 10^3
NO CALCULATORS!
II. Questions from last night's homework and completion of unfinished work
from yesterday
III. Introduction of logarithms and converting between logarithmic and exponential
form
A. Conduct whole-class discussion about evaluating 2^x=6...May need to note
2^2=4 and 2^3 = 9, so 2<x<3.
B. Briefly speak of John Napier, the inventor of logs.
C. When are we EVER going to use this?
Briefly explain about real-life applications of logarithms: decibels, Richter
Scale, Carbon Dating.
D. Logarithms are just exponents!
E. Go through example 1 in textbook while writing some of the following
on the board:
Logarithmic form Exponential form
log(2 )16=4 24=16
log 10=1 10^1=10
log(3 )1=0 3^0=1
log 0.1=-1 10^-1=0.1 or 1/10
log(4 )64=x _______
log(5) 125=y _______
log(7 )49=z _______
IV. Evaluating logarithmic expressions
log(4 )16
log(5 )1
log(9 )3
log(3 )-1
In whole class discussion, go through the answers to these problems. Ask
students how they got their answers and call some to the board to write
their methods down if necessary. Use exponential form, if necessary. Go
back to examples already written on the board (log4 64=x, log5 125=y, and
log7 49=z) and have students evaluate them for x, y, and z, respectively.
V. Special cases and quick things to point out
A. On the board or overhead, write:
log(a) 1=0 because a0=1
log(a) a=1 because a1=a
log(a) a^x=x because _____
Conduct a brief discussion as to what is to be written in the blank. (ax=ax)
B. Conduct a discussion as to why we cannot have base 1 nor take the log
of anything less than or equal to zero. Include in the discussion the following
examples:
Logarithmic form Exponential form
log(1) 500=x 1^x=500
log(3 )0 =x 3^x=0
log7 (-5)=x 7x=-5
C. Explain that log x can be written as log x. This is the common logarithm.
If time, show students on their graphing calculators that the "log"
button means log10. Have them evaluate on the calculator: log 1000000 and
log 106. Does 106 = 1000000? Explain that base 10 is the base used most
often in our lives.
VI. Change of base formula and wrap up.
A. Go back to the problem 2^x=6 and explain/conduct discussion on how to
solve. Confirm why we take log2 of both sides. log(2) 2^x=log2 6. So, x=
log2 6.
B. Observe with students that there is no way to enter base on many calculators
(specifically, the TI-82). Write the formula on the board for students to
use to find x:
So, log(2) 6 = log 6/log2 ª 2.585. Go through the formula with students.
Homework Assignment:
In textbook, p. 409: 1-5, 11-14, 15-33 odd, 37-39, 41-55 odd. Due next class
day (Monday, Feb. 17). See attached.
On homework, students MUST copy the problem down and show some work. Homework
will be graded A, B, C, F, or 0 based on effort.
Graphs and applications of logarithms
Goals: Reinforce evaluation of logarithmic expressions algebraically and
with calculators
Reinforce conversion between exponential and logarithmic form
Graph simple logarithmic functions
Use logarithms in a real-life situation
I. Warm-up
log(6) 36=x
log(3) 0=x
log(2) (-4)=z
log(2) 8=x
log(5) 125=x
log(3) x=4
log(2) (x+4)=5
II. Questions from last night's homework and completion of unfinished work
from yesterday
III. Graphs of basic logarithmic functions
With your graphing calculators graph y=log(2) x
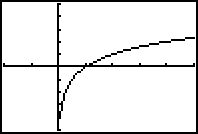
B. Conduct whole class discussion of how to graph this and other logarithmic
functions such as log x, log(5 )x. Use T-tables, graphing calculator and
dry-erase graph board. Have student volunteer show how to come up with the
graph without graphing it on the calculator. Be sure to note why we cannot
start the T-table with x=0 (When will 2^y=0?). Students should notice what
happens to the graph as base increases. Change of base formula may need
to be noted: . To make the T-table, exponential form will likely be used.
C. On graphing calculator, graph alog (x+b) +c, varying a, b, and c. Conduct
a class discussion about how varying these values affects the graphs.
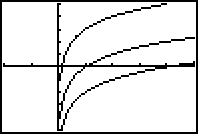
On the overhead you will see that the top curve is when you add c, and
the bottom curve is when you subtract c.
IV. Noticing inverse relations
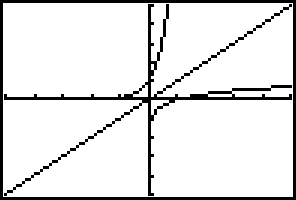
A. With students, graph y=log x on graphing calculators. (Make sure students
know this is logarithm base 10)
B. y=10^x. Notice anything?
C. y=x. Explain that these two functions are inverses of each other.
Real World Applications
Slope of a beach, s, is related to the diameter, d, of the sand particles
on it by this equation:
s=0.159+0.118log d.
Have students work in groups of 2 to find the slope when d=0.25. Have
student volunteer work it out on board. (Answer is roughly 9/100). Teacher
should sketch a rough graph of what the slope of the beach looks like. The
students can also use the trace key to find a solution. Tell the students
to get as close to .25 as possible.
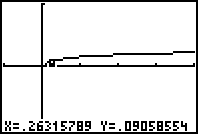
B. Have students evaluate d=0.125 (fine sand) in same groups. Have student
volunteer graph what the slope of the beach looks like.
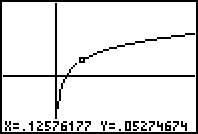
Homework Assignment:
1. In textbook, p. 409-411:6, 61-66, 69-77 odd, 79-83, 88-90. Due tomorrow.
(Tuesday, Feb. 18).
2. For extra credit, Mixed Review in textbook p. 412. Due in four class
days. (Friday, Feb. 21)
On homework, students MUST copy the problem down and show some work. Homework
will be graded A, B, C, F, or 0 based on effort. Evaluation scheme for the
Mixed Review has yet to be determined.
Goals/ Objectives:
-Students should be able to use properties of logarithms.
-Students should be able to expand and condense logarithms.
Lesson Plans:
When I introduced log properties I wanted the students to make a connection
with something that they already know; therefore, I had the following warm
up problems on the board:
1- 4^3 * 4^2 = 4*4*4*4*4= 45 2- 2^4 * 2^5 =
2*2*2*2*2*2*2*2*2= 512
3- 3^6/3^4 = (3*3*3*3*3*3)/(3*3*3*3)= (6-4) 32= 9
4- 7^2/7^5 = (2-5) = 1/73
5- (7^3)^2= (7*7*7)^2 = (7*7*7)(7*7*7)= 76
My goal for the students to come up with the following on their own.
Therefore a^na^m = a^(n+m) (a^n)^m = a^nm a^n/a^m = a^(n-m)
Log properties are formed the same way. This is still on the board:
a^na^m = a^(n+m) (a^n)^m = a^nm a^n/a^m = a^(n-m)
8.3 Properties of Logarithms
Goals/ Objectives:
-Students should be able to solve real- life problems using logarithms.
-Students will learn how to evaluate the intensity of earthquakes.
-Students will examine the patterns of decibels and intensity as they relate
to sound.
Lesson Plans:
On the overhead when the students enter the room:
Expand the following problems: Condense the following problems:
log16x log6- log3/2
log6/5 10 logx+ (2/3)log64
**Students will answer the questions at the board.
?? Any questions?
Name:____________________________
REAL- WORLD APPLICATIONS: DECIBEL LEVEL
For the following questions us the formula:
B= 10 log (I/I(0))
where B is the sound level in Decibels,
I is the intensity of the sound in watts per square centimeter,
I(0) is an intensity of 10^-16 watts per square centimeter.
1- What is the sound intensity in a conversation?
2- What is the sound intensity with the decibel level of 90? Where are you
when you experience this level of sound?
3- What is the sound intensity of a quiet room?
4- Choose 3 additional sounds you hear daily and estimate where you would
place them in the scale shown on the transparency.
8.3 Properties of Logarithms (T-I 82 Lab)
Goals/ Objectives:
-Students should be able to use their calculator to do logarithms functions.
Lesson Plans:
On the board when students come into class:
(Students to board)
1-Is the graph of y= 3(.25)^x exponential growth or exponential decay.
2-Use a calculator to evaluate log3 to three decimal places.
3-Evaluate log(5)6 following to three decimal places using the change-of-base
formula.
4-Expand log(x^3/y^4)
5-Condense log3+ 2logt
Today is a lab day.
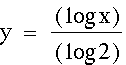
What happens around -3?
What is the domain and the range of log(x-7)- log (x+3)?
Solve for x: 2= log(x-7) + log (x+3)

Sketch the graph of 2= log(x-7)+og (x+3)
What happens around -3?
What is the domain and the range of log(x-7)+ log (x+3)?
The natural base e.
Goals: Students should know how to use the number e as a base of an exponential
function.
Students will use the natural base e in real-life applications
I. Warm-up
Identify the following functions as representing exponential growth or exponential
decay: f(x)=3(0.25)^x g(x)=2(2.1)^x
III. Introduction of the natural base e
A. Briefly mention Leonhard Euler, for whom e takes its name.
B. Show/describe that e=1/0! + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + 1/6! +
...
ª 2.718281828459
(may need to review factorial notation)
C. Review that x and y are examples of variables, but e is a number. If
time, show that it is irrational.
D. Have students evaluate eb for several values of b.
E. When are we EVER going to use this? Natural base e applies to interest
rates on accounts, air pressure, population, and radioactive decay.
IV. Simplifying natural base expressions
Briefly go over the rules of exponents which apply to e just as they apply
to any number or variable.
(e^2)(e^3) = e^2+3 = e^5
(6e^2)/(2e^1) = 3e^2-1 = 3e
e^-4 = 1/e^4
(2e^-1)^2 = 2*2^(e-2) = 4^(e-2) = 4/e^2
V. Graph of the base e function
A. Have students graph y=2^x and y=3^x, zooming in to see the graphs more
clearly.
B. Next, have students graph y=e^x. Ask them about where the graph of y=e^x
lies and why they think this must be so. 2<e<3.
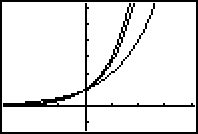
C. Go over some shifts of the y=ex curve. Graph y=Ce^bx +d + a varying
a, d and C at first, then b last. Lastly, make b negative to yield y=Cebx
. Let students discover that if b is negative, the function represents decay,
and if b is positive, the function represents growth.
D. Go through some examples of exponential decay and growth:
e^(6x),-3e^(6x),0.1e^(4x),3e^-x,-5e^-4x
VI. Using base e to growth of money with a continuously compounding interest
rate.
A. Recall with students the formula for compounding interest n times per
year: A=P(1+r/n)^nt. Prompt students for what the variables mean: A - balance,
P-initial principle, r- annual interest rate, n- number of times per year
that interest is compounded.
B. What if interest were compounded continuously, that is, roughly every
second?
A=Pe^(rt) where all the variables remain the same except we have no n.
C. Using the graphing calculator and previous formulas, go through second
example with students:
You just deposited $200 in a savings account which has an APR of 5.0%. If
interest were compounded continuously, what would the balance be after five
years ($256.81)? What if interest was compounded daily? ($256.80) Our y=
screen should look like this:
Now graph the function
Use your trace key to find x=5

Give other values for the students to find, so they will use the trace
key.
D. If time, go through more examples with students. Initial principle =
$5000, interest = 3%. Compare compunding semi-annually and continuously.
Note that with smaller initial deposits, the continuous compounding does
not differ much from compounding daily.
Homework Assignment:
In textbook, p. 423-425: 1-4, 9-21 odd, 25-32, 39-41, 45-52, 58-60.
On homework, students MUST copy the problem down and show some work. Homework
will be graded A, B, C, F, or 0 based on effort.
Review Day
Goals/Objectives: Students should be able to exhibit knowledge of the material
covered in the past 8 days (and, of course, all the days before).
Conduct the following review (which Parallels the test) and then open the
class to any other questions
Compare the following graphs?
y= 5x+7 y= 5(x+7)
Expand the following:
log(3/a) logx^4
Condense the following:
log3+ logx 7logb
The value of the new car you bought in 1990 for $17800 decreases by 16%
each year. What will the car be worth in 1998?
?? Does anyone have any other questions from your homework?
Evaluate to 3 decimal places
log(2) 32 log99
Solve for x
log(x) 64= 6 log2x + log25= 4
Is f(x)= 10.2e^.04t an example of exponential growth or decay?
$600 is deposited in an account that pay 7% annual interest compounded continuously.
Use the formula A= Pe^rt to find the balance after 10 years.
?? Does anyone have any other questions from your homework?
Homework: Study for test!!!
Assessment: I will be walking around helping the students that have any
questions.
Logarithms
Test A
Name__________________________ Date_________
1. Evaluate e^2 to three decimal places.
2. Compare the graphs of f(x)=3^x and g(x)=3^x+1.
3. Craig and Jessica bought a new car in 1984 for $16,000. The car's value
decreased by 13% each year. What was the car's value in 1992?
4. Solve for x. log 8 - (1/3)logx = log 2
5. Expand the expression log(4) 5x^2.
6. Condense the expression log(4) x - log(4 )5.
7. Solve for x. log(4) (1/16) = x
8. Which of the following is undefined?
log(3) 9, log(3) 1, log(3) (-3)
Why?
9. Evaluate log(6) 30 to three decimal places.
10. Solve for x. log7 2401 = x
11. Use the grid above to sketch the graph of f(x) = log(4) (x+1).
12. Evaluate 6^e to three decimal places.
13. Is f(x) = 13.7e^-0.04t an example of exponential growth or exponential
decay?
14. $1000 is deposited in an account that pays 7% annual interest compounded
CONTINUOUSLY. Use the formula A = Pert to find the balance after 10 years.