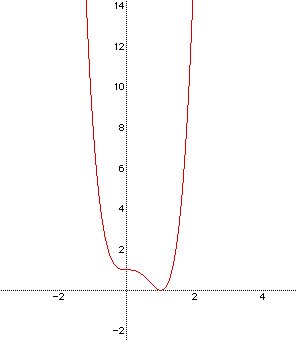

Let us think about the differential function ![]() because it will
give more significant information for the function
because it will
give more significant information for the function ![]() . The differential
function has two roots x=0, and x=1. So the function
. The differential
function has two roots x=0, and x=1. So the function ![]() has two points
where the derivatives are zero. That is to say, two tangent lines at two
different point are parallel to x-axis. See the next graph of
has two points
where the derivatives are zero. That is to say, two tangent lines at two
different point are parallel to x-axis. See the next graph of ![]() and
and
![]() .
.
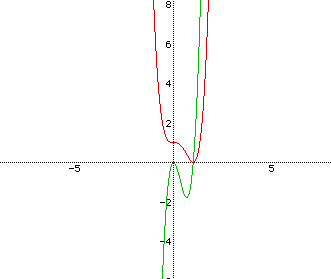
If x<0 , then vales of the differentiated function (green one) are
all negative. So any tangent line on ![]() (where x<0) has a negative
slope. And as x decreases from 0 the lopes of tangent lines should be decreased.
Students can compare these all facts from the above graph. There are three
changes in green graph.
(where x<0) has a negative
slope. And as x decreases from 0 the lopes of tangent lines should be decreased.
Students can compare these all facts from the above graph. There are three
changes in green graph.