OBJECTIVES: 1. To investigate relationships among variables.
2. To collect and analyze data.
3. To constuct and analyze tables.
4. To acquire a notion for what are acceptable and unacceptable approximations.
5. To envision the effects on graphs by changing the parameters in the algebraic representation of the function.
6. To determine domain and range for a real world problem.
MATERIALS: Cardstock to make telescope
Meter stick
ACTIVITY
PREPARATION: 1. Students should work in groups of 3.
2. Form the telescope from 2 pieces of cardstock rolled up. Each rolled up piece should be about 25 cm long. Each part should be about 2 cm in diameter.
3. Insert one of the rolls into the other to make the telescope. The shortest telescope will be 25 cm long, and the longest should be approximately 50 cm long.
ACTIVITY: Their are 3 different investigations for this activity. Two of the investigations deal with direct variation (linear functions). One of the investigations deal with inverse variation (hyperbolic functions).
General Instructions for the 3 Investigations:
In all 3 investigations, we are interested in examining how changing different parameters for our telescope changes how much we are able to view through the telescope. In the experiment, a meterstick is secured to a wall. One student stands a given distance from the wall and looks through the telescope. Another student places 2 fingers on the meterstick to mark a range. The student looking through the telescope will tell what range he is able to see. The third student should record the number of centimeters seen.
INVESTIGATION #1:
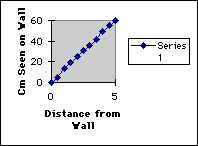
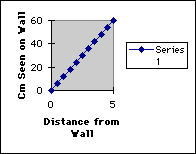
For this experiment, the students should keep the diameter and the length of the telescope constant and vary the distance the student is standing from the wall from 0 to 5 meters by increments of one-half.
INVESTIGATION #2:
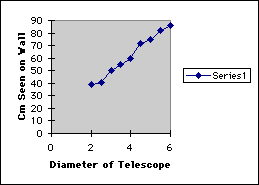
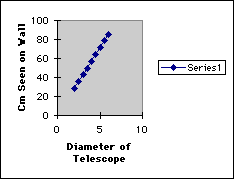
For this experiment, the students should keep the distance from the wall and the length of the telescope constant and vary the diameter of the telescope from 2 to 6 cm by increments of one-half.
INVESTIGATION #3:
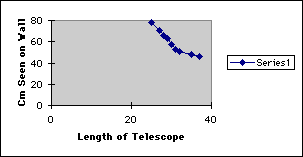
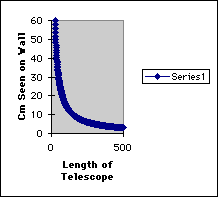
For this experiment, the students should keep the distance from the wall and the diameter of the telescope constant and vary the length of the telescope from 25 to 50 cm by increments of 1 cm.
DISCUSSION &
EXPLORATION: After recording the data, the class could be led into the discussion of what a function is and what dependent and independent variables are. Students should be able to identify and classify the variables in the 3 investigations.
Questions: * What is constant?
* What things are changing?
* What is the dependent variable?
* What is the dependent variable?
* Does the dependent variable increase, decrease, or remain constant as the independent variable increases?
Have students conjecture based on the data and their discussion of these questions what the graphs of the 3 functions would look like.
To test the conjectures about the graphs, students can plot their data
from the 3 investigations on a graphing calculator or preferably using a
spreadsheet application. The first 2 investigations should produce a linear
graph, while the third graph should look like a hyperbolic curve. Three
possible graphs follow: 


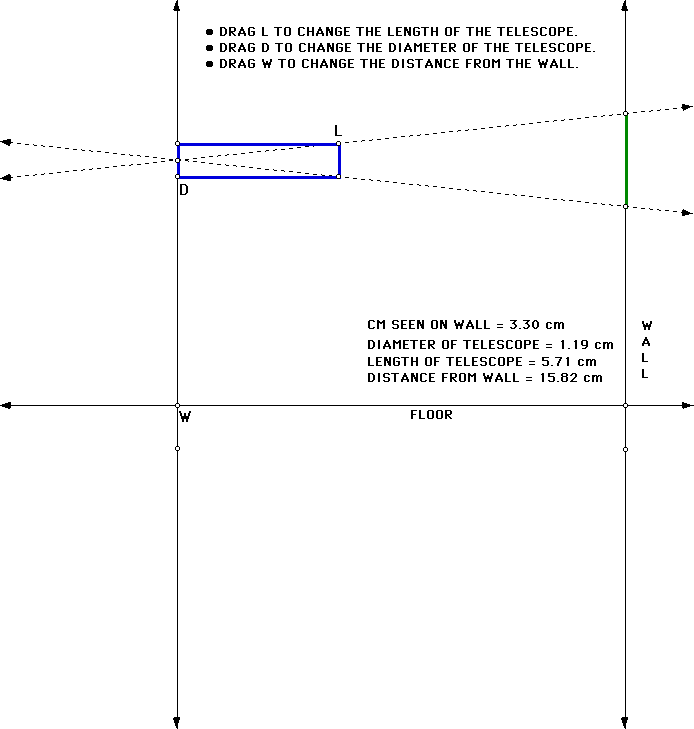
From the spreadsheet, the teacher can model the investigations with a GSP demonstration. The GSP sketch could be made available for each student to change the parameters on the telescope and take note of the changes in the amount of wall that can be seen. Students could construct this demonstration on their own depending on their familiarity with GSP.
Question: How can we write an expression for the relationship between the variables in each of the investigations?
To help answer this question, students can model the telescope experiment
with a GSP sketch. 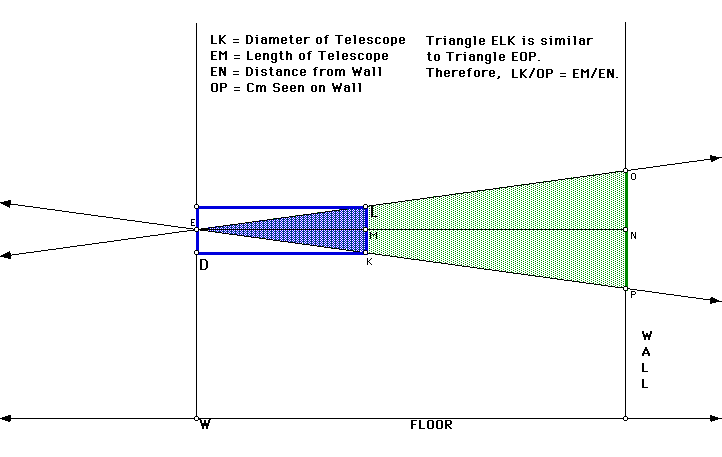
In the sketch, the eye's view forms similar triangles, ELK and EOP. We then have the proportion LK / OP = EM / EN. Solving for the CM Seen on the Wall (OP) we have,
OP = (LK*EN) / EM. Let LK = d, EN = w, and EM = l.
Questions: * In each investigation, what are the constants?
* If we let x = the independent variable and y = the dependent variable, what will the expressions for the functions look like?
#1: y = (d/l)(x) with d, l constant
#2: y = (w/l)(x) with w, l constant
#3: y = (dw)/x with d, w constant
Once the students have discovered this equations, they can go back to the spreadsheet and enter the equation as a formula to generate points and also graph. With the spreadsheet they can also change the constants to notice the changes in the data and graphs.The following graphs are from Microsoft Excel:
Students can also graph the equations on Algebra Xpresser and investigate for different constant values. The graphs could lead to a discussion of domain and range for the real world problem, and the restrictions that the real world puts on the function. Here are the Xpresser graphs for the 3 investigations:
# 1 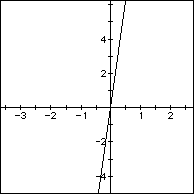 #2
#2 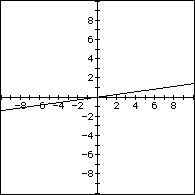 #3
#3 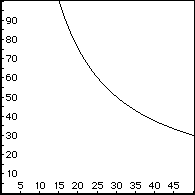
Cooney, Thomas J. Integrating Mathematics Pedagogy and Content in Teacher Education: Functions. 1993