Essay 1
In the Korean classrooms, Geometry is not taught as an independent curriculum as in United States. Geometry is included in mathematics textbooks just as a part of whole structure of mathematics curriculum. So the idea of spending a whole year in studying Geometry in the secondary school is very unique to me. And the degree of importance about Geometry in secondary school education is somewhat less than Algebra-related problem solving. I can imagine Geometry stressed more in Korean classrooms when combined with applicable technology like Geometer's Sketch Pad. It will save time and energy which were used in constructing mathematical figures with a compass and a straightedge.
I had a idea of experimenting "a pedal curve" from EMT 668 class, fall quarter 1995. We learned some characteristics of a pedal triangle. In this paper, I want to teach students to find a pedal curve, a particular kind of locus. In this article, I am going to try to find a pedal curve with a circle and a point which is inside of a circle, on a side of the circle, or outside of the circle. It will be an interesting experience to students. They are encouraged to use GSP while trying to construct a pedal curve. Of course, the definition of a pedal curve will be given but the main purpose of this essay is to explore some pedal curves with GSP and to have specific experience of students themselves through the processes.
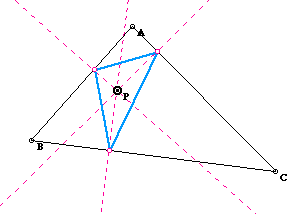
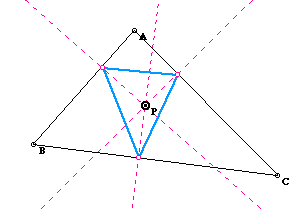
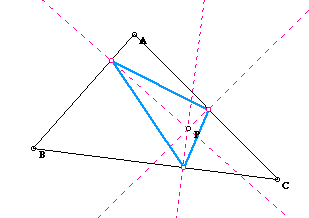
Let's recall a pedal triangle. As we see in the following picture, for any given point inside of a triangle ABC, we draw the perpendicular lines to each side of the triangle, then we can have a pedal triangle by connecting three points on three sides of a triangle.



I moved the location of P above. What did you find? The locus of the
pedal curve with a triangle is also triangles although the shape of blue
triangle was changed in terms of the location of P.
Now, I will give the definition of a pedal curve. A pedal curve is
the locus of the feet of the perpendiculars from the point to the tangents
to the given figure. A pedal curve is always drawn from a point to some
geometric figure.
Now, here is a challenge! What do you think of the locus of the pedal curve
with a circle? Is it the same kind of figure that is given to you? In the
above example, the pedal curve with a triangle and a point inside the triangle
is also a triangle. Let's say that you are supposed to find a pedal curve
with a circle and a point outside of the circle. Is it going to be another
circle? What kind of figure are you going to see? Let's explore!!

First you need above setting in GSP. A is the point that you want with
a point B on the circle. So we now know that the pedal curve for this case
would not be totally inside of the circle. What do you expect to have? Let's
go further.

We can trace the point A with moving B on the circle with GSP. Doesn't
it look cool? Yes, it is.
The next figure is a complete pedal curve with a circle and a point out
side of the circle. It it is not a kind of a circle.
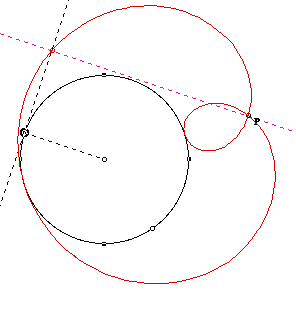
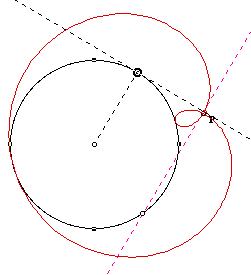
Let's see the shapes of the pedal curves above while moving the position
of P. The interesting question here is if we make P approach closer to the
circle. What will happen to a small loop?
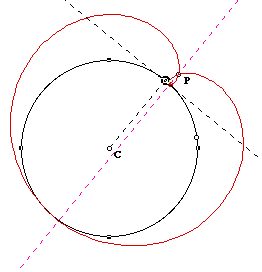
The result is following. As P approaches to the circle, the small loop gets
smaller and smaller . And if we put P on the circle, the loops disappears.
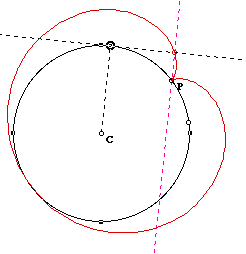
Even though we put P on the circle, we do not have a circle-shape pedal
curve. It is just a closed figure.
What about the case of a circle and a point which is inside of the circle?
There are two cases of the position of the point generally. One is an arbitrary
point P inside of the circle, and another is the case
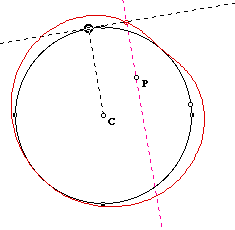
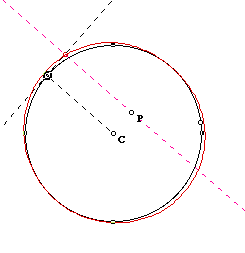
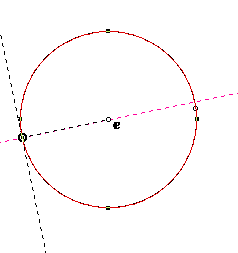
In the case of a point on the center of the circle, we have the circle
itself as the pedal curve. Every tangent line on a point on a circle decides
the pedal point. See the following picture.
I've thought of pedal curves with various figures. Unfortunately,
GSP couldn't draw a tangent line on a eclipse. (This turns out to be
wrong by the help of Dr. James Wilson in my department.)
But the process in this paper shows enough interesting connection between
mathematical idea and actual construction of students themselves. Especially,
the part where GSP can trace the point and animate gives us a clear identification
about the concept that teachers want to address.