Introduction
We were working on a group project for EMT 708 in which we examined curriculum development material. High School Mathematics and Its Applications (HiMAP) is a curriculum development project which has produced modules for high school teachers. Applications of Geometrical Probability by Fred C. Djang is one of the modules produced by HiMAP. One of the problems presented in Applications of Geometrical Probability looked very interesting and could be presented in the mathematics classroom visually using GSP.
The Problem
Given a circle with diameter 2, what is the probability that the length
of a chord drawn will exceed ![]() ?
?
In the way the question is posed, there are several different models which could be looked at to examine this problem. Depending on which model is chosen, several different solutions can be found. We will examine three models and the solutions for each of the models presented.
Model 1
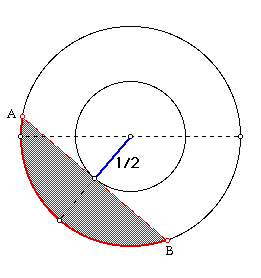
In Model 1, the radius of the inside circle is 1/2 and that of outside
circle is 1. Thus, we have by the Pythagorean Theorem the length of half
of the chord is ![]() /2. So we obtained
/2. So we obtained ![]() as the length of the chord.
If the chord passes through the inside circle, then the length of AB will
exceed
as the length of the chord.
If the chord passes through the inside circle, then the length of AB will
exceed ![]() . If the chord does not pass through the inside circle, then
the length of AB is less than
. If the chord does not pass through the inside circle, then
the length of AB is less than ![]() . Here, AB is tangent to the inside
circle and we can rotate AB around the inside circle. With this interpretation,
we can define the probability as below.
. Here, AB is tangent to the inside
circle and we can rotate AB around the inside circle. With this interpretation,
we can define the probability as below.
Probability=Measure of the Feasible Region/Measure of the Sample Region
= Area of the Inner Circle / Area of the Outside Circle
= 1/4
We obtained 1/4 as a solution. Do you feel satisfied with it? However, we can think of another approach in which we can come up with a different solution. Of course, we need a different model.
Model 2
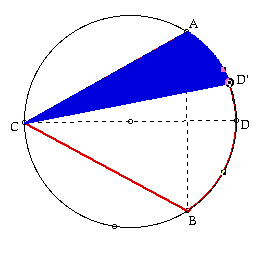
In this model, the endpoint, D', of the chord CD' can be moved along
the circumference of the circle from the fixed point C. Since any angle
inscribed in a semicircle is a right angle, we have that ACD is a right
triangle. Thus, if the angle ACD is [[pi]]/6, then the angle ADC is [[pi]]/3.
So, now we can apply the relationship between the ratio of the three angles
[[pi]]/3, [[pi]]/6, and [[pi]]/2 and that of the three lengths ![]() ,
1, and 2, respectively. Sincethe diameter of the circle is 2, we have the
length of chord AC is
,
1, and 2, respectively. Sincethe diameter of the circle is 2, we have the
length of chord AC is ![]() . We have the desired probability when the chord CD'
moves along the arc ADB.
. We have the desired probability when the chord CD'
moves along the arc ADB.
Probability=Measure of the Feasible Region/Measure of the Sample Region
= Length of Arc ADB / Circumference of the Circle
= 1/3
We obtained a different solution compared with Model 1. But we can not tell which one is right or wrong because the models that we examined are different. Now let us examine one last model.
Model 3
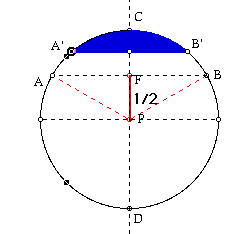
In this model, the chord A'B' is perpendicular to the diameter CD.
As the chord A'B' moves from the point C and down to the chord AB. Since
the length of PB is 1 and lengsh of FP is 1/2 the lengh of the chord A'B'
is ![]() . The Pythagorean Theorem gives us BF is
. The Pythagorean Theorem gives us BF is ![]() /2 and hence AB
is
/2 and hence AB
is ![]() . The desired probability is obtained when the chord A'B' starts
moving from AB to the point P.
. The desired probability is obtained when the chord A'B' starts
moving from AB to the point P.
With this interpretation, we can define the probability as below.
Probability =Measure of the Feasible Region/Measure of the Sample Space
=Length of FP/Length of CP
=1/2
In examining this problem, choosing the diameter of the circle to
be 2 and the length of the chord to be the ![]() makes the problem accessible
to students. Students can use their knowledge of high school geometry in
solving the problem. As the parameters of the problem are changed in each
model, the nature of the solution changes. Students are encouraged to find
other approaches which generate other solutions. Teachers can use this idea
to develop extensions to this problem.
makes the problem accessible
to students. Students can use their knowledge of high school geometry in
solving the problem. As the parameters of the problem are changed in each
model, the nature of the solution changes. Students are encouraged to find
other approaches which generate other solutions. Teachers can use this idea
to develop extensions to this problem.
If you want to go back to my homepage, click
here