Exploration with the centers of a triangle and three equilateral triangles
on each side
by Kyungsoon Jeon
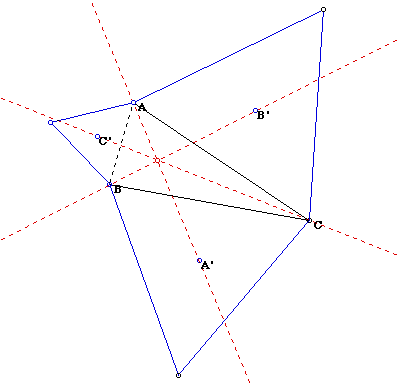
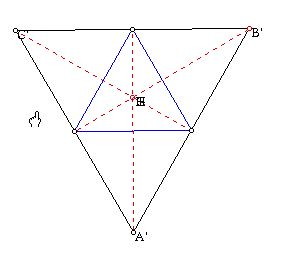
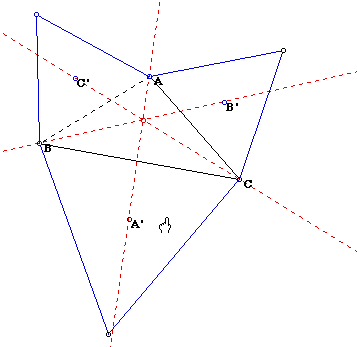
A. Take any triangle ABC. Construct equilateral triangles externally on each side and locate the centroid of each equilateral triangle. Label these centroids A', B', and C' for the triangle centroids opposite angles A, B, and C. Construct lines AA', BB', and CC'.

The lines AA', BB', and CC' are concurrent. Let me label this point F. If we find the orthocenter, centroid, incenter, or circumcenter of triangle ABC we can know that the point F is not the same with any of centers of triangle ABC.
If we change the shape of triangle ABC in many ways, one of interesting things is that the point F is always nearer to the incenter I than any other centers of triangle ABC.
B. Let me repeat the investigation using a square constructed externally on each side of triangle ABC and with A', B', and C' being the centers of the squares.
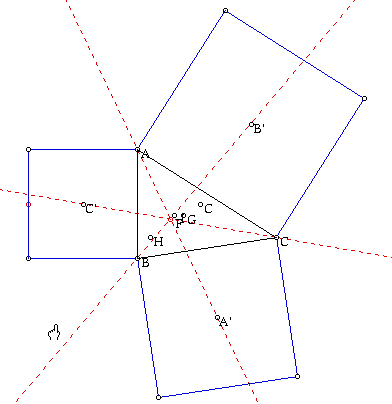
Here again, the lines are concurrent.
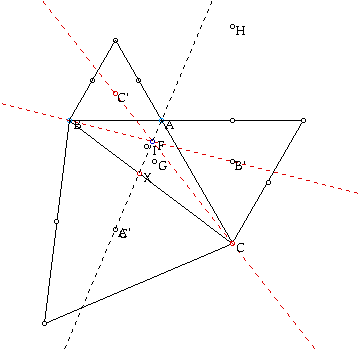
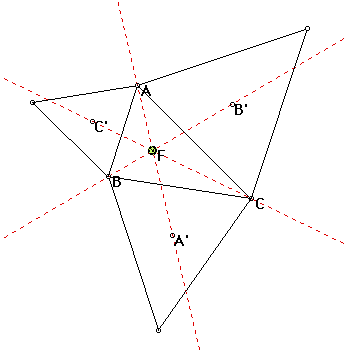
C. Let me repeat the investigation in A but let A', B', and C' be the external vertices of the externally constructed equilateral triangles with A' off the side opposite vertex A, etc.
They are also concurrent and not the any centers of triangle ABC either. I will label the concurrent point F.
If the triangle ABC is an equilateral triangle, every center of triangle ABC (i.e O,G,I,C) exists in the same point and also F meets there.
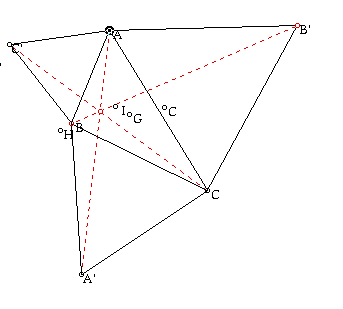
D. If an isosceles triangle with height equal to the side is constructed on each side, they are concurrent as we can see on the picture below.
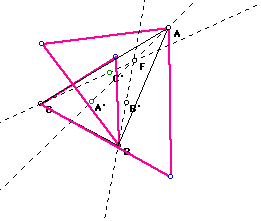
E. I repeat A with the equilateral triangles constructed toward the interior of triangle ABC. Here the three triangles overlap.
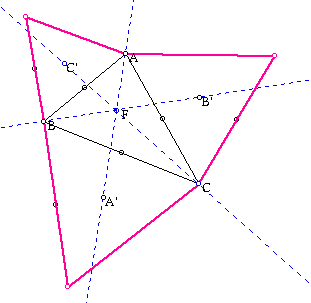
But the lines AA', BB', CC' are concurrent. And if triangle ABC is an equilateral triangle, the four triangles are the same therefore the concurrent point is the centroid, incenter, circumcenter and orthocenter of triangle ABC.
F. I will propose further extensions of this investigation.
(1) Take any triangle ABC. Construct equilateral triangles externally on each side and locate the circumcenter of each equilateral triangle. label these circumcenters A',B', and C' for the triangle circumcenters opposite angles A, B, and C.
(2) Repeat a similar investigation with (1) constructing incenters of each equilateral triangle.
(3) Repeat a similar investigation with (2) locating orthocenters of each equilateral triangle.