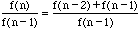
The Spreadsheet in Mathematics Explorations
Fibonacci Sequence
by Kyungsoon Jeon
Working with different types of number arrays can be one of interesting activities in a mathematics classroom. A sequence which is called " Fibonacci Sequence " is one of many famous sequences. As technology comes into a classroom students also need to learn many different mathematical topics dealing with different technologies.
The Fibonacci Sequences is the following array of numbers.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987...
When the numbers are given, students will be able to generate the rule of the sequence through examining several adjacent numbers .They will say that each term is the sum of the two preceding terms.
In this paper, I will treat many different aspects of the Fibonacci Sequence by generalizing the relationship of numbers, making a data with spreadsheet, drawing a chart for the data, extending the ratio of each pair of adjacent terms to the golden ratio, examining the ratio of every second term, every third term, and so on, and understanding the algebraic characteristics of the results by examining with Algebra Xpresser.
Let's construct the numbers in Fibonacci Sequence by the rule. It must be a time-consuming work for every student. Calculators are allowed to be used here.
1, 1, 2, 3, 4, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181,...
We can express the Fibonacci Sequence using symbol of functions.
f(0)=1, f(1)=1
f(n)=f(n-2)+f(n-1)
As n increases, we get the Fibonacci numbers. Let's divide the equation by f(n-1)
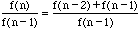
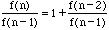
If the concept of limit is introduced and n becomes large, then the equation can be expressed as the following.
x=1+
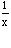
x2=x+1
To get the approximate idea of two roots of the equation. We can look at the graph of two functions, y = x2 and y = x + 1. The Algebra Xpresser is used for the graphs.
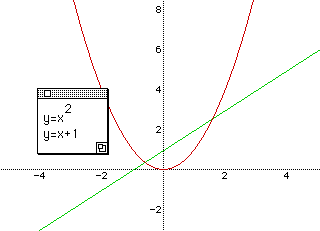
The positive root of the equation exists between 1.5 and 2.
To get the exact roots of the equation, we use the quadratic formula for x2 = x + 1. Then,
x=
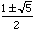
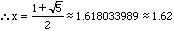
We can get a number 1.62 which is very familiar to us. It is the golden ratio.
Let's make a table of the Fibonacci numbers by using a spreadsheet. The data will also show the Fibonacci numbers, the ratio of each pair of adjacent terms, every second term, every third term and so on.
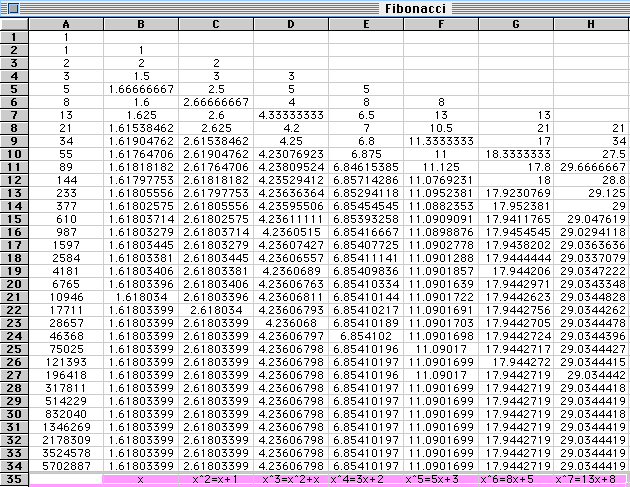
In particular, we can draw a chart for the ratios of adjacent Fibonacci numbers.
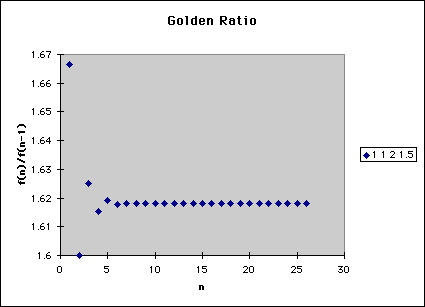
As further exploration, we can draw a chart for all ratios which is shown in the chart.
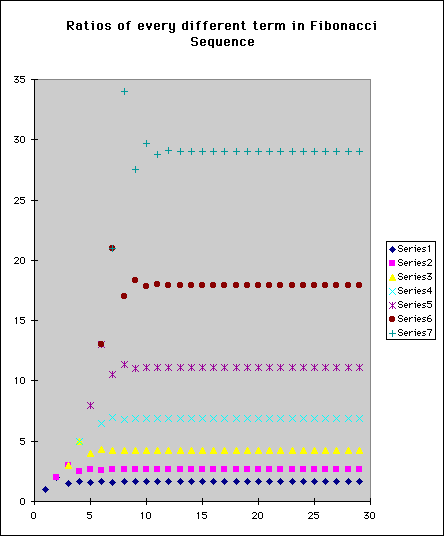
The ratios shows the Fibonacci ratios are in geometric progression. If we call the ratio of each pair of adjacent terms as x, then the ratio of every second term is x2. And x2 be solved by x+1. Similarly, the ratio of every third term is x3, and it can be solved by 2x + 1.
x: the ratio of each pair of adjacent terms
x2 = x + 1
x3 = 2x + 1
x4 = 3x + 2
x5 = 5x + 3
x6 = 8x + 5
.
.
.
Let's make a new sequence with 1 and 5 as the first and second number of the sequence.
The construction of members of a sequence takes the rule of that of Fibonacci sequence.
Here is the array of the numbers. 1, 5, 6, 11, 17, 28, 45, 73, 118, 191, 309, 500, ... which is called a Lucas Sequence. We can express this sequence using the symbol of functions, too.
f(0)=1, f(1)=5
f(n)=f(n-2)+f(n-1)
Though we do not follow the same dividing process by f(n-1). We can know that the ratio would be the same as that of the Fibonacci Sequence because the terms are generated by the same rule. So functions have the same forms.
Here is a chart for the ratios of adjacent numbers in my new sequence.
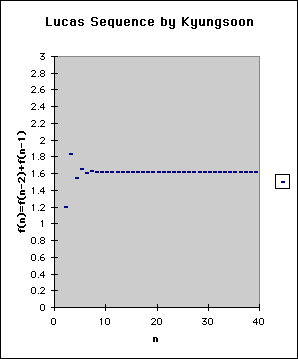
It also the golden ratio.
As we have seen in this paper, students can use any one of many different approaches that they have learned in their mathematics classes.. If we actively start combining various mathematical knowledge with different mathematical approaches, our mathematics classroom will be the place filled with students' creativity and interest and students will gain more confidence about problems with the added technique.