Question : For what values of p does the equation x3+ px + 1 = 0 have
three real roots? Extend for other values of q.
If we just think of the roots of the equation then students may need a great deal of algebraic skill. But the purpose of introducing a computer and mathematical programs in a classroom is not just for students to obtain the exact answers of a problem with paper and pencil but to have students explore and discover mathematical ideas and use the technology to solve problems.
Let's look at the equation x3+ px + 1 = 0 first. It is cubic equation. So it can be a difficult for students to graph of the function where students can get the idea of the roots of the equation visually.
First, let's decompose the equation.
x3+1 = -px
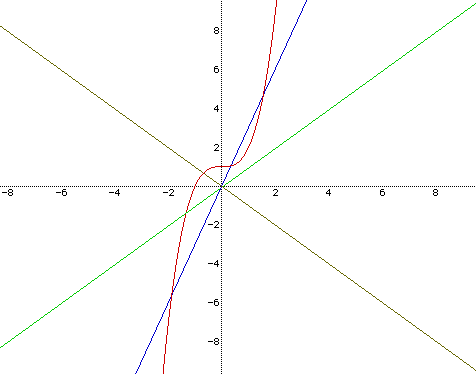
We can think of two functions from the equation above. let y = x3+1 and y = -px .
we want to obtain the value of p which makes the equation have 3 real roots. Since we can graph the function of y = x3+1 easily, what we will do is to analyze the information of the graph of y = -px. The graph of y = -px goes through the origin (0,0) no matter of the value of -p. So we can change the position of the graph of y = -px and see the intersections of y= x3+1 and y = -px.

Here, -p can not be negative. Because if it is negative then the two graphs can not intersect at three places. Hence -p should be at least positive. From now on let -p be P for the convenience. So P should be a positive number. See what happens when P=2. Let's graph the two function of y = x3+1 and y = 2x by using Algebra Xpresser. The graphs are as follows.
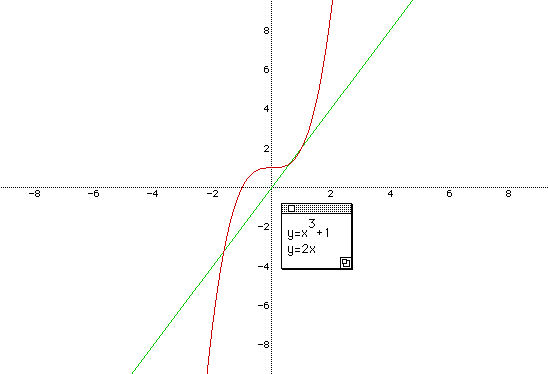
Two graphs meet at three different points. Let's try other values
to P to see if we can find other intercepts. y= ![]() and y =
and y = ![]() are drawn below.
are drawn below.

Here we need to examine the vales of P between ![]() and 2. Since
the graph of y = x3 +1 and y = Px do not intersect when P=
and 2. Since
the graph of y = x3 +1 and y = Px do not intersect when P= ![]() and do intersect
when P= 2 at three different places. See the next figure.
and do intersect
when P= 2 at three different places. See the next figure.

To get more information about P, we can use the Zoom-In process. That is to say, a portion of the graphs of y = x3+ 1 and y = Px can be enlarged. So we can check that if p = 2, then the equation has three real roots visually. Students also can use the Zoom-In process to make sure that y= 2x intersects y=x3+1 at the three different points as shown below.

How about the case of P= ![]() ? Let's graph y = x3 + 1, y =, y
=
? Let's graph y = x3 + 1, y =, y
= ![]() x and y = 2x.
x and y = 2x.
We could check by the Zoom - In process that the equation has three
real roots when P is ![]() .
.
Now we can understand that P should be approximately greater than 2 to give three real roots. So far we have seen one approach. Let's think of another approach to examine values of p for all roots of the equation x3 + px + 1 = 0. We will examine the graph of the equation in the x and p-plane. Our interest is to find out the possible change of p so that p= -x2 - 1/x.

In the above picture, if p is greater than -2, then we just have one real root. But if p is smaller than -2, then we get three real roots. (here, we need to understand that p=-2 is also not the exact border to make the equation have three real roots)
Let's go back to the equation x3+ px + q = 0. Now let's change the q, and see the graph of p = -x2 - q/x. We will also take advantage of Algebra Xpresser .
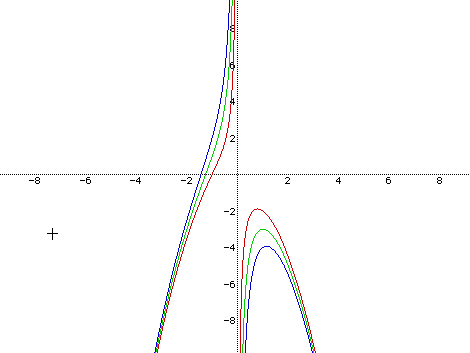
As q becomes larger, p has to be smaller than -2. We have generalize for p>0 to make the equation p = -x2 - q/x have three real roots.
Let's consider the case of q<0. How does p change as q decreases like -1, -2, -3...? See the following graphing.
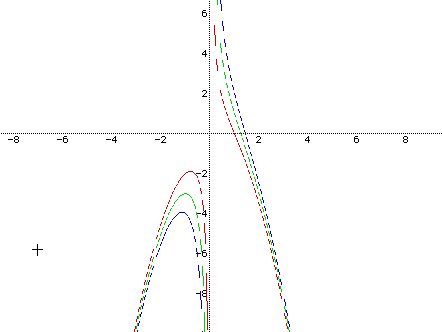
We have the switched graphs for q<0 compared with q>0. As q decrease p should be also decreased. It can be generalized as the following. For the equation p= -x 2 -q/x to have three real roots, as |q| becomes larger p must become smaller.
So we see the value of these kinds of activities. Computers enable us to graph numerous functions quickly and establish common properties of classes of functions. In the past these activities were usually not possible because of the time required to produce accurate graphs. Now, we can have students play with the three-dimensional space. We are able to have students explore and discover mathematical concepts, and use graphs to solve problems. See the next figure for a reference. It shows an interesting extension of further exploration of the equation x3+ px + q = 0.

If you want to go back to my homepage, click
here