(The primary source for this essay is "Mathematical Recreations: Fibonacci Forgeries," by Ian Stewart, published in Scientific American, May 1995. Mr. Stewart has several interesting mathematical concepts in this column, which appears periodically.)

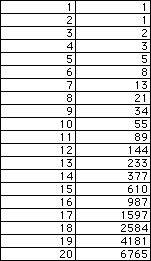
The Fibonacci sequence is the very famous sequence in which each number is the sum of the two previous numbers. The sequence starts with two 1's, and then precedes:

1, 1, 1+1=2, 1 + 2 = 3, ...

(Note: the following displays are on Microsoft Excel)

The applications involving Fibonacci sequences are endless. Sunflowers have rows of petals that are in pairs of 21 and 34, 34 and 55, 55 and 89, and some giant sunflowers have a row of 89 petals and a row of 144 petals, all consecutive Fibonacci numbers. Pine cones have 8 rows to the right and 13 rows to the left. Bees build their honeycombs using an adaptation of the Fibonacci sequence.

One problem that mathematicians face is that they must look at everything before jumping to conclusions. This can be very evident in the sequences. Consider the following sequence:

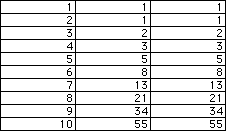
Looks like the Fibonacci sequence, doesn't it? But the next term in the sequence is 91! This is not consistant with Fibonacci, is it?

The point of this essay is that there exist sequences which start off like a Fibonacci sequence, but end up being an all new sequence. These are Fibonacci Forgeries, and the sequence above is an example. So what is the formula for this sequence?

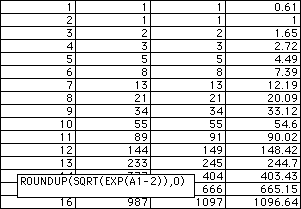
So, although this sequence is consistant with Fibonacci for ten terms, it is actually a Fibonacci Forgery. Let's look at some other sequences.

Consider the following sequence and it's rate:

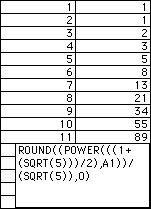
This starts off as Fibonacci, but if we continue it out, will we find the whole thing is Fibonacci? The answer is yes. This is not a Fibonacci Forgery but instead the real thing. Why? Well, Binet came up with the formula of

fn = [((1 + (51/2))/2)n + ((1 - (51/2))/2)n] / (51/2).

This formula is designed to find the nth term of the Fibonacci sequence.

Is the following sequence Fibonacci or forgery?

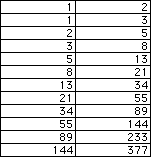
This sequence adds the first n terms of the Fibonacci sequence. As one can see, the sums of Fibonacci sequences results in another Fibonacci sequence.

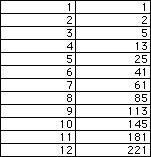
Another type of Fibonacci sequence is one in which the nth term is the sum of the squares of n-1 and n-2, so we have

1, 1^2 + 1^2 = 2, 1^2 + 2^2 = 5, 2^2 + 3^2 = 13, 3^2 + 4^2 = 25,... (see below)

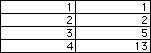
Now let's look to see if the following are Fibonacci or Forgery. This sequence sets the nth term a as

an = (n - 1) 2n-2 + 1

This starts off right, but look at the next few terms:

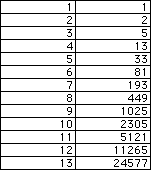
This sequence is another example of one that starts off like Fibonacci, but it is not really.

The purpose of this essay was to look at a few examples of Fibonacci sequences and Fibonacci forgeries. The desire of the writer is that those reading this will come away with the ralization that everything in mathematics should not be taken at face value. Given a sequence, if asked to find the next term, ask if it is Fibonacci befgore you say "89." The sequence might actually be something else entirely.

The moral of the story is: Look closely at what you are doing, make sure you know the rules, and don't assume anything (unless you state that, of course)!