By Fhonda Danley and September Matteson
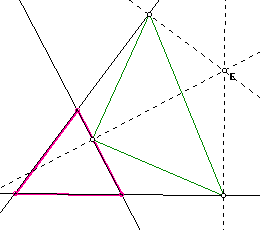
Given a triangle ABC and any point E in the plane, the triangle formed by the perpendiculars to the sides of ABC is called the Pedal triangle for the pedal point E. In the case below, triangle ABC is the pink triangle and our pedal triangle is the green triangle. Through investigations on GSP, since there is no restriction on our pedal point E, our pedal triangle will move anywhere whenever E moves or is moved.

Exploration.
Now we want to look at different circumstances for our pedal point E.
Let's suppose that our point E is the centroid of our triangle ABC. What happens to our pedal triangle?
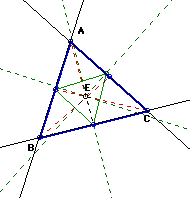
If E is the centroid, then our pedal triangle is created on the interior of ABC and remains the same triangle because since E is the centroid, it remains the same unless our triangle is changed. So in conclusion, our pedal triangle will never move outside of our triangle ABC. Now, let's investigate our triangles when our pedal point E is the incenter of ABC.
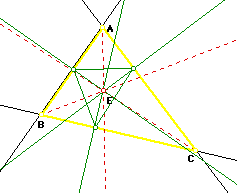
What we have here is another triangle inside of our original ABC. Also once again, our triangle remains in the same place and never moves because our point E is the incenter and will also never move. So, no matter what, a pedal triangle, when its pedal point is the incenter of triangle ABC, will be a stationary triangle on the inside of our triangle ABC. Now, let's investigate what happens when our pedal point E is also the orthocenter of the triangle.
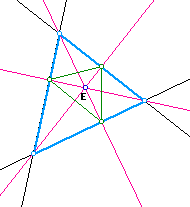
Here, we see that our pedal point E is the orthocenter of our triangle ABC (Light blue) . Our pedal triangle, green, is once again located inside of triangle ABC. From investigations on GSP, we know that because the pedal point is also the orthocenter, it will never change unless our original triangle ABC changes. So this triangle, pedal triangle, will never move outside of ABC. Now, let's look and see what happens when our pedal point is also the circumcenter of ABC.
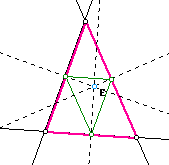
Once again, we see that our pedal triangle (green) is inside of our triangle ABC (pink triangle). Also again, we see that no matter what, because our pedal point is also the circumcenter, our pedal triangle will never move unless E moves or is moved. Now, let's investigate what happens when our pedal point is on a side of ABC.
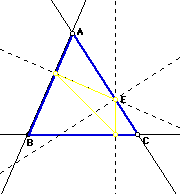
As we can see, once again our pedal triangle is inside of ABC. It is possible, however, for this triangle to move outside of ABC. As the point E or rather as point C of ABC is extended out, our pedal triangle begins to also move outward. See below how the pedal triangle is beginning to move outside of ABC while point E is still located on the side in the same place.
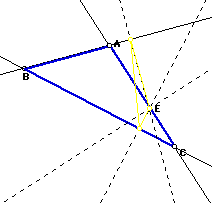
Now let's see what happens when E is one of our vertices of ABC.
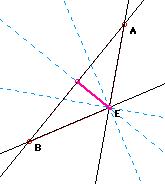
As we can see here, when our pedal point is one of the vertices of the triangle, we no longer get a triangle but instead we get a segment.
Now we want to investigate something called the simson line. This is where all of the three vertices of the pedal triangle are collinear. From our investigation on GSP, we see that as E approaches one of the vertices or becomes one of the vertices (as in the above example) of triangle ABC we do indeed get a line. This line can be called the simson line. The pictures below show what happens as E is approaching the vertices.
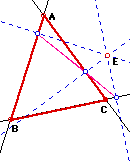
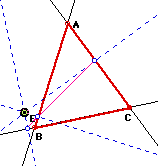
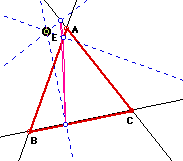
So, as we can see in all of the preceding pictures as E is approaching one of the vertices of ABC we do indeed get a line or rather a line begins to form. Now we want to construct a circle whose radius is larger than that of the radius of our circumcircle. We want to trace the midpoints as the pedal point moves around the newly constructed circle. What paths are our midpoints taking?
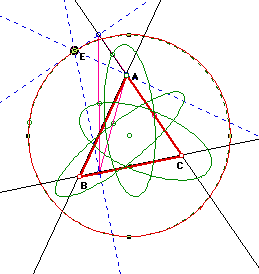
We can see that the midpoints of our pedal triangle are forming ellipses as our pedal point moves around the circle. What would happen if we were to let our circle be the actual circumcircle? Would we still obtain ellipses?
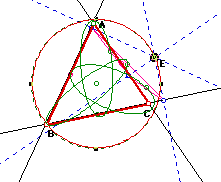
We see that we do indeed still obtain ellipses but the size of them is smaller than before. Let's see what happens as the radius of our circle also decreases.
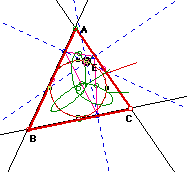
We can see that as our circle diminishes, we still obtain ellipses only they are much smaller. We will also conject that as our circles decrease in size, so will our ellipses. This last investigation concludes our explorations into pedal triangles. We hope that maybe we have given you some insight to do some investigations of your own concerning pedal triangles.