The point of this essay is to investigate the activity of parametric equations for different linear combinations of sine and cosine in the x and y equations. Figures 1-5 are graphs of equations of the forms
x(t) = a*cos(t) + h*sin(t)
y(t) = b*sin(t) + h*cos(t)
where a,b, and h are integers and 0 <= t <= 2[[pi]].
Figure 1 illustrates graphs with h = 0.
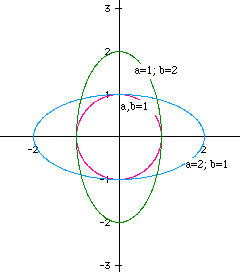
Figure 1

We see that for a = b = 1, a circle of radius 1 is obtained. Leaving a = 1 and changing b to 2, we get an ellipse centered at the origin with x-intercepts at 1 and -1 and y-intercepts at 2 and -2. Likewise if we leave b = 1 and change a to 2, we obtain an ellipse centered at the origin with x-intercepts at 2 and -2 and y-intercepts at 1 and -1. Notice that a (or the coefficient of cosine -- similar to the amplitude of cosine in a general equation) is equal to the absolute value of the x-intercepts of the graph.
Figure 2 illustrates an introduction of a non-trivial value of h.
Figure 2
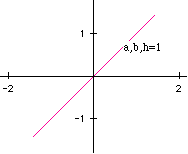
Figure 2 simply shows what happens with an h value of 1. By just looking at the finished graph, it appears that it is a segment of the line y = x (which I guess it is!), but while the graph was being drawn, it started at the origin at was completed in a "roundabout" fashion. (It almost looks as if it would produce an ellipse with z-intercepts in the xyz-plane.)
Figure 3
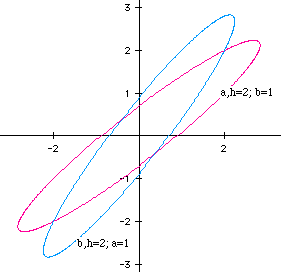
In Figure 3, h = 2, but in the two graphs, the values of a and b are reversed. This results in ellipses that are symmetrical about the line y = x. In my investigations, I saw that values of a, b, or h any higher than 3 had the same basic shape, but were just larger. Thus, I have decided to leave their pictures out of this discussion.
Figure 4
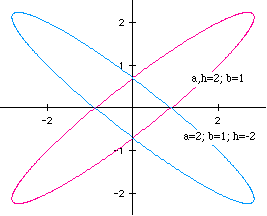
Figure 4 shows a and b held constant, but h at values of 2 and -2. As one can clearly see, these graphs are symmetric about the x- and y-axes.
Figure 5
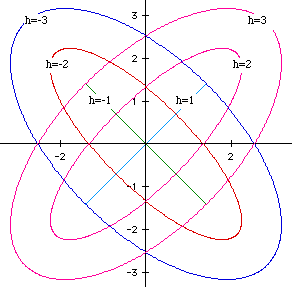
The last figure illustrates several graphs with h-values of +-1, +-2, and +-3. The graph of a parametric equation is meaningless without an interpretation of the axes upon which it lies. The positive half of the x-axis represents the zero position. If a segment (OP) had one endpoint at the origin and its other somewhere on the x-axis and the origin is assumed to be center of rotation, then a counter-clockwise rotation of OP of 90[[ring]] results in a rotation of [[pi]]/2 radians. (It acts very similar to the unit circle; actually, in Figure 1, where a,b=1, that IS the unit circle!)
Now, notice that where h=-1, h=2, and h=3 intersect at values of [[pi]]/4 + k*[[pi]], where k is any integer. (Here, the graphs of x(t) = a*cos(t) + h*sin(t); y(t) = b*sin(t) + h*cos(t) will be referred to by their h-values.) Likewise, the graphs with h=1, -2, and -3 intersect at values of (3*[[pi]])/4 + k*[[pi]], where k is any integer. This implies that the graphs on the cartesian plane of the above functions would intersect at these same values. Let's try it.
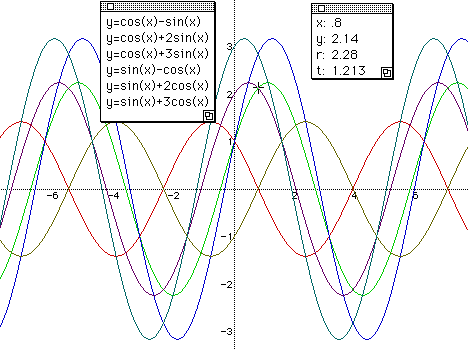
There it is. Notice that I placed the crossbar on one of the collinear intersections of the graphs. The x-value reads .8. The actual value of [[pi]]/4 is approximately 0.78539. If we add [[pi]], we obtain approximately 3.92699. Note that the next set of collinear intersections occurs just before x=4. It looks to be about right!
I wanted to explore the idea that our pair of parametric equations with nonzero, small, integral h-values was the locus of the vertex (x,y) of a triangle with altitude h when the other two vertices were moved about the x- and y-axes. So, I've made a GSP sketch to illustrate this...
Notice that when the sketch comes up, I have h set to equal exactly 1.000 inches. I also have b set to exactly 2.000 inches. When you run the animation, you obtain a tracing that is identical to the graph in Figure 2. Then, setting h to values close to 2 and 3 yields parts of an ellipse with wideness corresponding to their value of h. Very interesting!