
Department of Mathematics Education
J. Wilson, EMT 669

The Pythagorean Theorem was one of the earliest theorems known to ancient
civilizations. This famous theorem is named for the Greek mathematician
and philosopher, Pythagoras. Pythagoras founded the Pythagorean School of
Mathematics in Cortona, a Greek seaport in Southern Italy. He is credited
with many contributions to mathematics although some of them may have actually
been the work of his students.
The Pythagorean Theorem is Pythagoras' most famous mathematical contribution.
According to legend, Pythagoras was so happy when he discovered the theorem
that he offered a sacrifice of oxen. The later discovery that the square
root of 2 is irrational and therefore, cannot be expressed as a ratio of
two integers, greatly troubled Pythagoras and his followers. They were devout
in their belief that any two lengths were integral multiples of some unit
length. Many attempts were made to suppress the knowledge that the square
root of 2 is irrational. It is even said that the man who divulged the secret
was drowned at sea.
The Pythagorean Theorem is a statement about triangles containing a right
angle. The Pythagorean Theorem states that:
"The area of the square built upon the hypotenuse of a right
triangle is equal to the sum of the areas of the squares upon the remaining
sides."
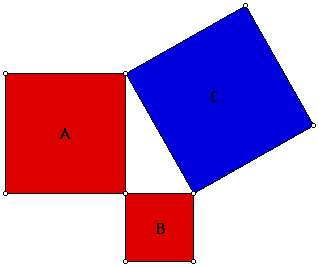
According to the Pythagorean Theorem, the sum of the areas of the two
red squares, squares A and B, is equal to the area of the blue square, square
C.
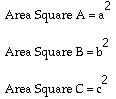
Thus, the Pythagorean Theorem stated algebraically is:
for a right triangle with sides of lengths a, b, and c, where c is the
length of the hypotenuse.
Although Pythagoras is credited with the famous theorem, it is likely that
the Babylonians knew the result for certain specific triangles at least
a millennium earlier than Pythagoras. It is not known how the Greeks originally
demonstrated the proof of the Pythagorean Theorem. If the methods of Book
II of Euclid's Elements were used, it is likely that it was
a dissection type of proof similar to the following:
"A large square of side a+b is divided into two smaller squares of
sides a and b respectively, and two equal rectangles with sides a and b;
each of these two rectangles can be split into two equal right triangles
by drawing the diagonal c. The four triangles can be arranged within another
square of side a+b as shown in the figures.
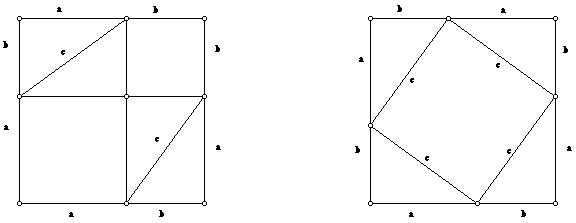
The area of the square can be shown in two different ways:
1. As the sum of the area of the two rectangles and the squares:
2. As the sum of the areas of a square and the four triangles:
Now, setting the two right hand side expressions in these equations equal, gives
Therefore, the square on c is equal to the sum of the squares on a and b.
(Burton 1991)
There are many other proofs of the Pythagorean Theorem. One came
from the contemporary Chinese civilization found in the oldest extant Chinese
text containing formal mathematical theories, the Arithmetic Classic
of the Gnoman and the Circular Paths of Heaven.
The proof of the Pythagorean Theorem that was inspired by a figure in this
book was included in the book Vijaganita, (Root Calculations), by
the Hindu mathematician Bhaskara. Bhaskara's only explanation of his proof
was, simply, "Behold".
These proofs and the geometrical discovery surrounding the Pythagorean Theorem
led to one of the earliest problems in the theory of numbers known as the
Pythgorean problem.
Find all right triangles whose sides are of integral length, thus finding
all solutions in the positive integers of the Pythagorean equation:
The three integers (x, y, z) that satisfy this equation is called a Pythagorean triple.
Some Pythagorean Triples:
x y z
3 4 5
5 12 13
7 24 25
9 40 41
11 60 61
The formula that will generate all Pythagorean triples first appeared in
Book X of Euclid's Elements:
where n and m are positive integers of opposite parity and m>n.
In his book Arithmetica, Diophantus confirmed that he could get right
triangles using this formula although he arrived at it under a different
line of reasoning.
The Pythagorean Theorem can be introduced to students during the middle
school years. This theorem becomes increasingly important during the high
school years. It is not enough to merely state the algebraic formula for
the Pythagorean Theorem. Students need to see the geometric connections
as well. The teaching and learning of the Pythagorean Theorem can be enriched
and enhanced through the use of dot paper, geoboards, paper folding, and
computer technology, as well as many other instructional materials. Through
the use of manipulatives and other educational resources, the Pythagorean
Theorem can mean much more to students than just
and plugging numbers into the formula.
The following is a variety of proofs of the Pythagorean Theorem including
one by Euclid. These proofs, along with manipulatives and technology, can
greatly improve students' understanding of the Pythagorean Theorem.
The following is a summation of the proof by Euclid, one of the most famous
mathematicians. This proof can be found in Book I of Euclid's Elements.
Proposition: In right-angled triangles the square on the hypotenuse
is equal to the sum of the squares on the legs.
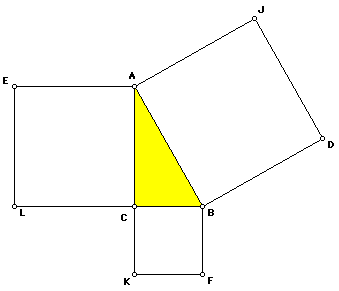
Euclid began with the Pythagorean configuration shown above in Figure
2. Then, he constructed a perpendicular line from C to the segment DJ on
the square on the hypotenuse. The points H and G are the intersections of
this perpendicular with the sides of the square on the hypotenuse. It lies
along the altitude to the right triangle ABC. See Figure 3.
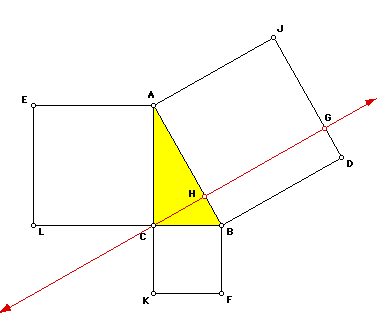
Next, Euclid showed that the area of rectangle HBDG is equal to the area of square on BC and that the are of the rectangle HAJG is equal to the area of the square on AC. He proved these equalities using the concept of similarity. Triangles ABC, AHC, and CHB are similar. The area of rectangle HAJG is (HA)(AJ) and since AJ = AB, the area is also (HA)(AB). The similarity of triangles ABC and AHC means
and therefore
or, as to be proved, the area of the rectangle HAJG is the same as the areaof the square on side AC. In the same way, triangles ABC and CHG are similar. So
and
Since the sum of the areas of the two rectangles is the area of the square
on the hypotenuse, this completes the proof.
Euclid was anxious to place this result in his work as soon as possible.
However, since his work on similarity was not to be until Books V and VI,
it was necessary for him to come up with another way to prove the Pythagorean
Theorem. Thus, he used the result that parallelograms are double the triangles
with the same base and between the same parallels. Draw CJ and BE.
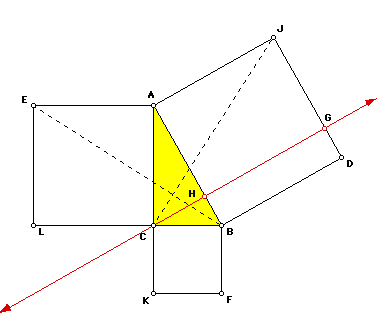
The area of the rectangle AHGJ is double the area of triangle JAC, and
the area of square ACLE is double triangle BAE. The two triangles are congruent
by SAS. The same result follows in a similar manner for the other rectangle
and square. (Katz, 1993)
Click here for a GSP animation
to illustrate this proof.
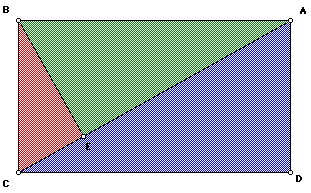
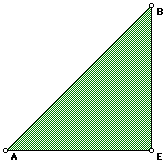
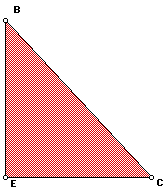
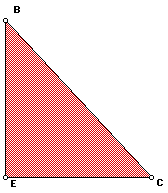
It can be seen that triangles 2 (in green) and 1 (in red), will completely
overlap triangle 3 (in blue). Now, we can give a proof of the Pythagorean
Theorem using these same triangles.
Proof:
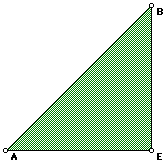
I. Compare triangles 1 and 3.
Angles E and D, respectively, are the right angles in these triangles.
By comparing their similarities, we have
and from Figure 6, BC = AD. So,
By cross-multiplication, we get :
II. Compare triangles 2 and 3:
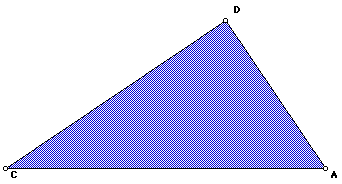
By comparing the similarities of triangles 2 and 3 we get:
From Figure 4, AB = CD. By substitution,
Cross-multiplication gives:
Finally, by adding equations 1 and 2, we get:
From triangle 3,
so
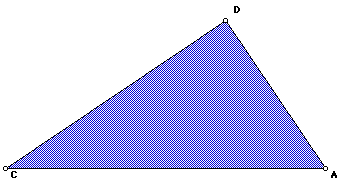
We have proved the Pythagorean Theorem.
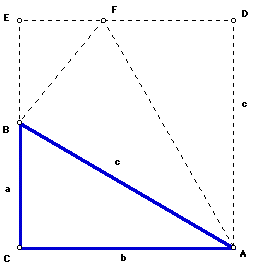
Next, since m<EBF + m<ABC + m<ABF = 180 degrees and m<ABF
= 90 degrees, <EBF and <ABC are complementary. Thus, m<EBF + m<ABC
= 90 degrees. We also know that
m<BAC + m<ABC + m<ACB = 180 degrees. Since m<ACB = 90 degrees,
m<BAC + m<ABC = 90 degrees. Therefore, m<EBF + m<ABC = m<BAC
+ m<ABC and m<BAC = m<EBF.
By the AA similarity theorem, triangle EBF is similar to triangle CAB.
Now, let k be the similarity ratio between triangles EBF and CAB.
.
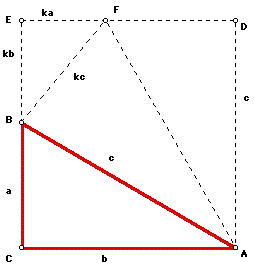
Thus, triangle EBF has sides with lengths ka, kb, and kc. Since FB = FD, FD = kc. Also, since the opposite sides of a rectangle are congruent, b = ka + kc and c = a + kb. By solving for k, we have
Thus,
By cross-multiplication,
Therefore,
and we have completed the proof.
Next, draw CD perpendicular to AB as shown in the next figure.
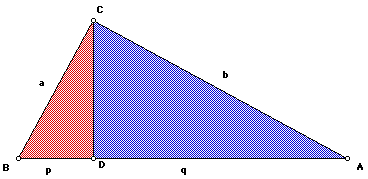
Triangle 1
Compare triangles 1 and 3:
Triangle 1 (green) is the right triangle that we began with prior to constructing
CD. Triangle 3 (red) is one of the two triangles formed by the construction
of CD.
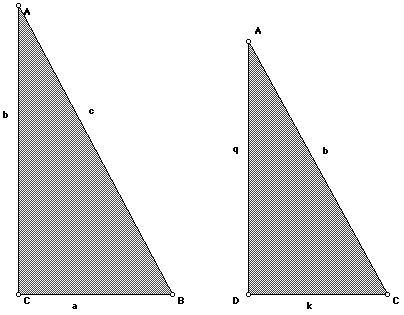
By comparing these two triangles, we can see that
Compare triangles 1 and 2:
Triangle 1 (green) is the same as above. Triangle 2 (blue) is the other
triangle formed by constructing CD. Its right angle is angle D.
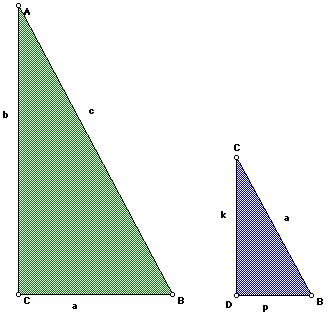
By comparing these two triangles, we see that
By adding equations 3 and 4 we get:
From Figures 11 and 12, with CD, we have that (p + q) = c. By substitution,
we get
The next proof of the Pythagorean Theorem that will be presented is one
in which a trapezoid will be used.
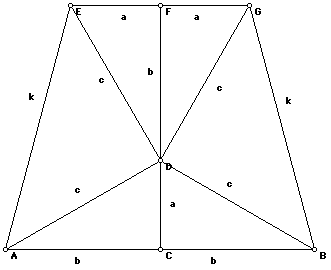
By the construction that was used to form this trapezoid, all 6 of the
triangles contained in this trapezoid are right triangles. Thus,
And by using the respective formulas for area, we get:
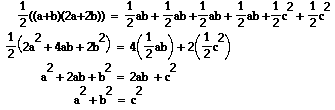
We have completed the proof of the Pythagorean Theorem using the trapezoid.
In this Pythagorean configuration, the square on the hypotenuse has been
divided into 4 right triangles and 1 square, MNPQ, in the center. Since
MN = AN - AM = a - b. Each side of square MNPQ has length of a - b. This
gives the following:
Area of Square on the hypotenuse = Sum of the Areas of the 4 triangles
and the Area of Square MNPQ
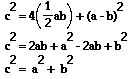
As mentioned above, this proof of the Pythagorean Theorem can be further
explored and proved using puzzles that are made from the Pythagorean configuration.
Students can make these puzzles and then use the pieces from squares on
the legs of the right triangle to cover the square on the hypotenuse. This
can be a great connection because it is a "hands-on" activity.
Students can then use the puzzle to prove the Pythagorean Theorem on their
own.
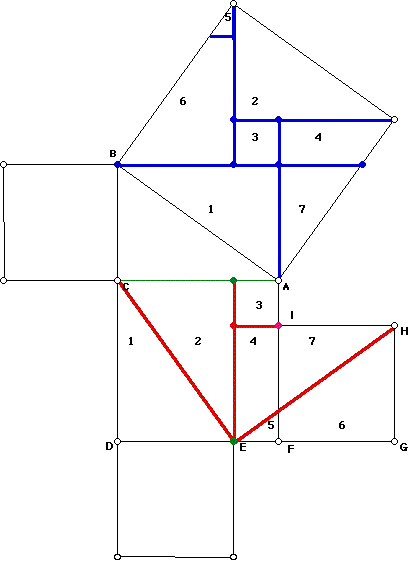
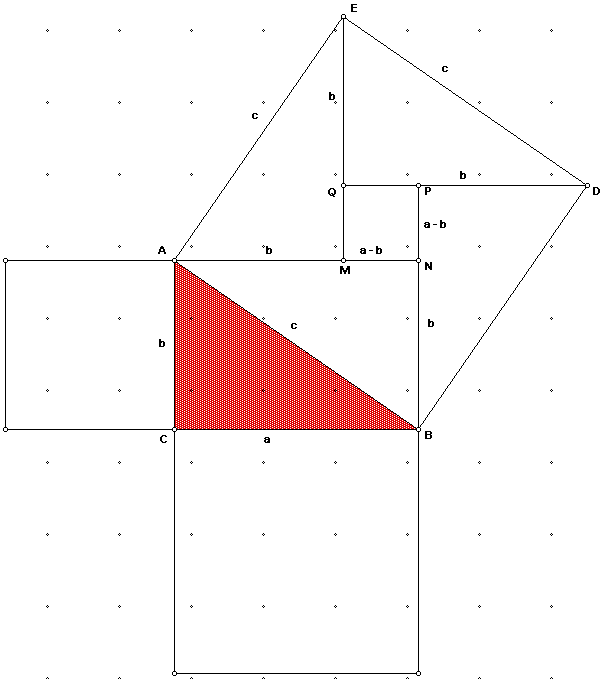
To create this puzzle, copy the square on BC twice, once placed below the
square on AC and once to the right of the square on AC as shown in Figure
17.
Proof Using Figure 17:
Triangle CDE is congruent to triangle ACB by leg-leg.
In triangle ACB, m<ACB =90 and the sides have lengths a, b, c.
In triangle CDE, m<CDE =90 and the sides have lengths a,b, c.
Triangle EGH is congruent to triangle ACB by leg-leg. The m<EGH =90 and
its sides have lengths a and c. Since EF=b-a=AI, EG=b. Thus the diagonals
CE and EH are both equal to c.
(Note: Pieces 4 and 7, and pieces 5 and 6 are not separated.)
By calculating the area of each piece, it can be shown that
Area 1:
Area 2:
Area 3:
Area 6 (and Area 5):
Area 7 (and Area 4):
By adding all of these areas together we get the following result:
and
Thus, we have proved the Pythagorean Theorem for the puzzle.
Beamer, James E. . Using Puzzles to Teach the Pythagorean Theorem:
Mathematics Teacher. May 1989; NCTM : Reston,VA.
Burton, David M. . Burton's History of Mathematics: An Introduction (Third
edition). 1991; William C. Brown Publishers: Dubuque, IA.
deLemos, Jamie. The Pythagorean Theorem: Mathematics Teacher. January
1995; NCTM : Reston,VA.
Hoehn, Larry. A New Proof of the Pythagorean Theorem: Mathematics
Teacher. February 1995; NCTM: Reston, VA.
Katz, Victor J. . A History of Mathematics. 1993; Harper Collins:
New York, New York.
Lufkin, Dan. . The Incredible Three-by-Five Card! : Mathematics
Teacher. February 1996: Reston, VA.