
The Pentagon Problem
by
Stephanie J. Morris
The "Pentagon Problem" begins with any pentagon. A second pentagon,
in blue, is formed by connecting the midpoints of each side of the first
pentagon. A third pentagon, in green, is constructed the same way by connecting
the midpoints of pentagon 2.
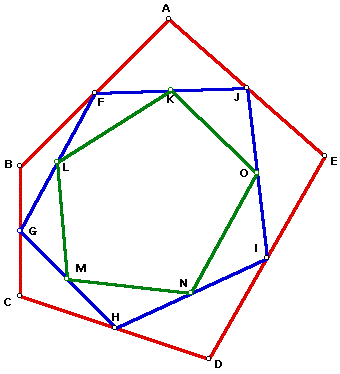
Conjecture:
"As long as each side of the two smaller pentagons
are formed by joining the midpoints of the next larger pentagon,
the two ratios of the areas will always be equal, and the two ratios of
the perimeters will always be equal, no matter what shape the largest pentagon
has."
Do you think that this conjecture is valid? Why or why not?
When I first read this conjecture, I thought that it seemed pretty "logical"
that the conjecture was a valid one. I believed that after several constructions
of various pentagons and the comparisons of the above mentioned ratios,
that I could come up with a proof of this conjecture.
However, after I began investigating the conjecture with the Geometer's
Sketchpad, I soon learned that maybe my own assumptions of the conjecture's
validity and its proof were not so logical after all.
Investigation of Pentagons:
I began with an arbitrary pentagon, i.e. it is not a regular pentagon. I
then constructed the other two pentagons according to the guidelines of
the problem. The original pentagon, pentagon 1 is in red. Pentagon 2 is
in blue and pentagon 3 is in green.

At first glance, it seems that the conjecture just might be true. There
appears to be a constant ratio between the Area of the Pentagon and the
area of the pentagon from which it was constructed.
For example:
Area Pentagon 3 = .65 Area Pentagon 2 = .65
Area Pentagon 2 Area Pentagon 1
After seeing this, I conjectured that the same ratio would hold when comparing
the area of pentagon 3 and the area of pentagon 1. I thought that it would
hold since pentagon 3 is constructed from pentagon 2 which is constructed
from pentagon 1. It seemed that since pentagon 3 is indirectly constructed
from pentagon 1, that they would be related in the same way also.
Area Pentagon 3 = .42
Area Pentagon 1
After seeing that the ratio did not hold, I realized that it did not make
sense for it to hold. I conjectured that the ratio would not be constant,
but that perhaps there would be a constant relationship between the areas
of pentagon 3 and pentagon 1. For instance, a fractional relationship. Maybe
I would discover this when I changed the shape of the original pentagon
later in my investigation.
Next, I decided to look at the ratios of the perimeters of pentagons 1,
2 , and 3.
Perimeter 2 = .80 Perimeter 3 = .81
Perimeter 1 Perimeter 2
These ratios were very close, but not exactly equal. It seemed
likely that the minute difference could be attributed to the way that the
measurements were rounded off by Geometer's Sketch Pad. I decided that the
next pentagons that I looked at would not have measurements rounded off
until the thousandths place. I was curious to see what the ratio would be
between the perimeter of pentagon 3 and the perimeter of pentagon 1.
Perimeter 3 = .64
Perimeter 1
Once again, this comparison yielded a ratio that was not the same as the
ratios between the other pentagons when they were compared.
I was beginning to doubt the validity of the original conjecture. The ratios
were "approximately equal", but not exactly equal. Exactly equal
seemed to be what the conjecture called for.
The next thing that I decided to do was to change the shape of the original
pentagon from which the other two pentagons were formed. I wondered what
the effects would be on the area and perimeter ratios.
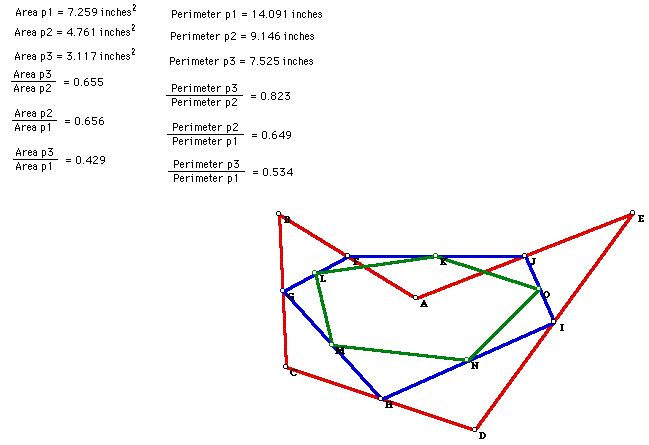
In this investigation, note that all measurements are measured to the thousandths
place. I did this so that I could see just how close the ratios are to being
equal. I was suspicious that some of the ratios might appear to be equal
when in fact, they may have been rounded-off and not equal at all. In doing
this, my suspicions were somewhat confirmed. For area, the ratios were very
close, but not truly equal. So, rounding-off the measurements does make
a big difference.
However, the perimeter ratios were not even close to being equal.
Area 3 = .655 Area 2 = .656
Area 2 Area 1
Area 3 = .429
Area 1
The perimeter ratios were very surprising and very contradictory to the
conjecture.
Perimeter 3 = .823 Perimeter 2 = .649
Perimeter 2 Perimeter 1
Perimeter 3 = .534
Perimeter 1
In this pentagon, the perimeter ratios were nowhere close to being constant.
Changing the shape of the original pentagon seemed to make the ratios become
even further apart. This seemed to be a strong counterexample to the conjecture.
I continued changing the shape of the original pentagon. In some cases,
it remained a pentagon and in other cases I changed it to a quadrilateral
or a triangle. The results were the following:

In this figure, the ratios of area between 3 and 2 and 2 and 1, were approximately
equal, but not exactly equal. The ratio of area between 3 and 1 is not close
to being the same. The same results were true for the perimeter ratios.
In this figure, I changed the pentagon to a quadrilateral.

The ratios here seem to be even further apart than before. For area, the
ratios that we are looking for to be constant differ by .02. In perimeter,
the ratios differ by .038! It seems that changing the shape of the original
pentagon does nothing to validate the conjecture, but rather it only casts
more doubt about its validity. I was convinced that the ratios were not
constant, and thus, that the conjecture is false. However, I wasn't sure
why the ratios were so close, yet unequal.
I decided to compare a few more figures before I made an "official"
decision about my thoughts on the conjecture.
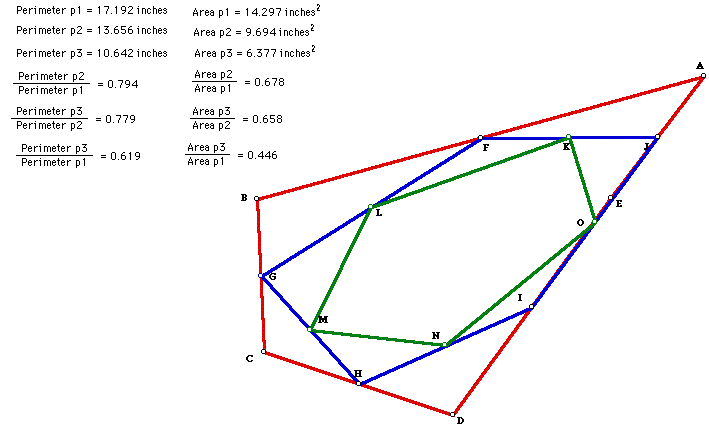
I changed the original pentagon to a quadrilateral, but one of a different
shape than in the above example. The differences in the ratios that were
"supposed" to be constant continued to become larger.
Here, the original pentagon was changed to a triangle. The results are consistent
with what I had found before. The ratios just were not constant.

While I had long since decided that the conjecture could not be true, there
was one more approach that I wanted to try, just to see what would happen.
I constructed a fourth pentagon in the same manner that I had constructed
pentagons 2 and 3.

Doing this, I had a lot of ratios to compare. I will discuss the area ratios
and the perimeter ratios separately. When I compared the area of the pentagon
and the area of the pentagon that it was constructed from, e.g., the area
of pentagon 3 and the area of pentagon 2, the ratios were all very close
to being equal. (See ratios 1,2, and 3.) However, when I compared the ratios
of the areas of a pentagon and a pentagon that it was not directly constructed
from, but certainly a consequence of, the ratio ws not similar to the above
mentioned ratios. For example, ratio 4 is not close to ratios 1-3, but upon
constructing ratio 5, I saw that ratio 4 and 5 are very close. Ratio 5 is
the same type of comparison as ratio 4. Ratio 5 is comparing the area of
pentagon 4 to the area of pentagon 2. Pentagon 4 was not directly constructed
from pentagon 2, but it is a consequence of pentagon 2 at the very least.
This was another relationship between the areas that needed to be explored.
A final ratio was constructed. Ratio 6 is the comparison of the area of
pentagon 4 and the area of pentagon 1. Again, pentagon 4 was not directly
constructed from pentagon 1, but pentagon 1 was certainly necessary in the
construction of pentagon 4. Again, the ratio was not approximately equal
to any of the other ratios that I had found

I went on and constructed a fifth pentagon from the fourth pentagon to see
what the ratios would turn out to be. The ratio of pentagon 5 to pentagon
1 was not close to the other ratios. This was not a surprising result since
pentagon 5 is not directly constructed from pentagon 1. This is the same
relationship that I discussed in the previous figure when comparing pentagon
4 to pentagon 1. Pentagon 1 is 3 pentagons "ahead" in the construction
than pentagon 4. I found the ratio of pentagon 5 to the pentagon that it
is 3 "ahead" of in the construction, pentagon 2.
Area p5 = .2798 Area p4 = .276 (3 apart)
Area p2 Area p1
This ratio is approximately the same as the ratio between pentagon 4 and
pentagon 1. I wondered if I might find more similar ratios when comparing
ratios of pentagons that are x pentagons apart in the construction.
Area p3 = .422 Area p4 = .427 (2 apart)
Area p1 Area p2
This was very fascinating to me. While the original conjecture was false,
I had discovered some other properties of the pentagons. When looking at
the original ratios of pentagons that are 1 apart in the construction, I
had found that they were not equal, but very close. I had found the same
to be true when looking at the ratios of the pentagons that are x apart
in the construction. I wanted to know what would happen if I continued to
construct more pentagons and x became larger than 4. Going back to the previous
figure, I constructed more pentagons and compared the ratios.

By constructing a sixth pentagon, I was able to compare the ratios of pentagons
that are 1. 2. 3. and 4 pentagons apart. Ratios of pentagons that are the
same number apart are all approximately equal. For instance:
Area p5 = .181 Area p6 = .183 (4 apart)
Area p1 Area p2
These ratios are approximately the same. Seeing this, I constructed yet
a seventh pentagon.
 The seventh pentagon and the ratios that can be formed
from it, fit well into my observation about x apart pentagons. In fact,
the newest ratios in each class here, are equal to the previous ratio in
the class. The class being x and x being the number of pentagons apart in
the construction.
The seventh pentagon and the ratios that can be formed
from it, fit well into my observation about x apart pentagons. In fact,
the newest ratios in each class here, are equal to the previous ratio in
the class. The class being x and x being the number of pentagons apart in
the construction.
Not wanting to spoil a good thing, I went on to construct an eighth pentagon.

This construction also backed my conjecture about the different "classes"
of the pentagons and the ratios contained within each class.
Constructing a ninth pentagon and examining class 7, my "class"
observation also held.

The following figure contains the tenth and final pentagon that I constructed.
By constructing this pentagon, I was able to form class 8 which also confers
with the observations that I had made earlier about the different classes
of pentagons and the ratios within each class.


In this figure, I examined the ratios of the perimeters of different pentagons
in the different classes. Rather than listing all of the individual ratios,
I have opted to list the results since the ratios are the of the same pentagons
that I examined above. After examining the perimeter ratios, I found that
the same results were true as were for the area ratios. By looking at the
perimeter ratios of the pentagons that were all x apart in the construction,
I discovered that the ratios within each class were all approximately equal
and that they usually converged to one value, ( in the picture above this
value is the last one listed). This was true for x= 1 - 8.
Even though I concluded that the original conjecture was not true, and thus,
was unable to offer a formal proof of the conjecture, I learned a great
deal about the area and perimeter of pentagons. I did many investigations
and came up with an "altered" version of the original conjecture:
"Altered" Conjecture: "As long as each
side of the smaller pentagons are formed by joining the midpoints of the
next larger pentagon, the ratios of the areas of the pentagons that are
x pentagons apart in the construction will all be approximately equal, and
the ratios of the perimeters of the pentagons that are x pentagons apart
in the construction will all be approximately equal."
There are many other avenues that can be explored with this investigation.
For example, the problem could be extended to the construction of other
polygons, including those that are regular and those that are not. Whatever
direction this problem takes, I think that it is certainly a worthwhile
problem for students to explore in mathematics.
Bibliography
Zbiek, Rose Mary. The Pentagon Problem: Geometric Reasoning
with Technology : Mathematics Teacher . February 1996,
NCTM: Reston, VA.












 The seventh pentagon and the ratios that can be formed
from it, fit well into my observation about x apart pentagons. In fact,
the newest ratios in each class here, are equal to the previous ratio in
the class. The class being x and x being the number of pentagons apart in
the construction.
The seventh pentagon and the ratios that can be formed
from it, fit well into my observation about x apart pentagons. In fact,
the newest ratios in each class here, are equal to the previous ratio in
the class. The class being x and x being the number of pentagons apart in
the construction. 


